# range ってなに?
# 1. 簡単に言えば...
例えば range(10) は 0 から 9 の自然数の集まりです。
for i in range(10):
print(i)
...
0
1
2
3
4
5
6
7
8
9
>>>
range オブジェクトは以下のように
添字表記 r[i] でも参照することができます。
これの方が数字の集まり感があります。
r = range(10)
r[0]
r[1]
r[2]
r[3]
r[4]
r[5]
r[6]
r[7]
r[8]
r[9]
10 未満の自然数の集まりと考えられそうです。
Python で言う自然数は後者に該当しそうです。
range(最大値)
自然数を 1, 2, 3, … とする流儀と、0, 1, 2, 3, … とする流儀があり、 前者は数論などでよく使われ、後者は集合論、論理学などでよく使われる
自然数 - Wikipedia (opens new window)
# 2. 正確に言えば...
range は英語で「範囲」を意味していているので range(90, 100, 2) は、 90 以上 100 未満の範囲の中にある等間隔 2 で並んでいる数字の集まりと考えると良いかもしれません。
for i in range(90, 100, 2):
print(i)
...
90
92
94
96
98
>>>
もうちょっと難しい言葉を使うと、下界、上限とか言ってもいいのかもしれません。
range(下界, 上限, 間隔)
# 3. 2つの疑問
range には2つの大きな疑問があります。 まず、なぜ 0 からはじまるのでしょうか? 次に、なぜ最小値以上で最大値未満なのでしょうか?
range が 0 からはじまるのが疑問でした。 なぜならすごく読み辛くなるからです。 例えば range(10) なら 1, 2, ... 10 として欲しいです。
Python は range(10) を 0, 1, ... 9 にしました。 range(10) は 0 からはじめる必要はあったのでしょうか?
# Python の選択
list(range(10)) == [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
# これでも良かったんじゃないの?と思ってしまうのです。
list(range(10)) == [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
それについて2つの観点から考えていきます。
# 4. 数学の観点から
答え: 数字の「範囲 range」を綺麗に表せるから
よく range を等差数列と表現している箇所が見られます。 range の概要を掴むときは、それがわかりやすいと思います。
しかし、なんで 1 じゃなくて 0 から始まるの?とか なんで「以下」じゃなくて「未満」なの?について考えるときは
range は「範囲」を表していると考えると良さそうです。
# 4.1. 理由
この箇所は以下の記事を参考にして書きました。 以上、未満という選択については、Dykstra という有名な人の以下の文献が元になっていると思われます。
Dykstra の文献では以下の4つの書き方を比較検討してくれています。 Dkystra と Python は a を選択しました。なぜでしょうか? 個人的には c がわかりやすそうな気がします。
2, 3, ... 12 の数字の範囲range
を表現する方法を考える
a. 2 <= i < 13 range(2, 13)
b. 1 < i <= 12 range(1, 12)
c. 2 <= i <= 12 range(2, 12)
d. 1 < i < 13 range(1, 13)
# Step 1. なんで未満なのか
Python の書き方、「以上」と「未満」なら、以下の2つを綺麗に表現できます。
# 1) 個数を綺麗に表現できる。
len(range(1, 3)) == -1 + 3
# 2) 0 からはじまる空の範囲も綺麗に表現できる。
list(range(0, 1)) == []
しかし、もし「以上」と「以下」にしてしまうと、この2つを綺麗には表現できません。
# 1) 個数を綺麗には表現できない。
len(range(1, 3)) == -1 + 3 + 1
# 2) 0 からはじまる空の範囲も綺麗に表現できない。
list(range(0, ?)) == []
以下のように書けばいいのかもしれませんが、
これだと自然数ではない数 -1 がはいってきます。
list(range(0, -1)) == []
また Dykstra の記述にはないのですが range(12) を
range(0,3), range(3,7), range(7,12) に分割することを考えて見ます。
すると以上、以下にすると、間が空いてしまうのです。
そんなに大した話ではないのですが。
意味合い的に...

# Step 2. なんで 0 からはじまるのか
「以上」、「未満」で決めると range(n) には2つの可能性があります。
range(n) == range(0, n)
range(n) == range(1, n+1)
上と下を見比べると確かに上の方が綺麗そうなので 0 から始めた方が良さそうですね。
1 から添字を書き始めた場合は a の表記に従うと添字の範囲が 1 <= i < N+1 となる; しかしながら 0 から始めれば 0 <= i < N となり、より良い。
Adhering to convention a) yields, when starting with subscript 1, the subscript range 1 <= i < N+1; starting with 0, however, gives the nicer range 0 <= i < N.
Why numbering should start at zero (opens new window)
# 4.2. 一貫性
僕はネットでダイクストラの説明を見ても「えー」としか思えませんでした。
(ひとつ前の、いまは消された答えで参照されていた) ダイクストラの記事は数学的には意味がありますが、 プログラミングをする時には、それほど関連性がありません。
While Dijkstra's article (previously referenced in a now-deleted answer) makes sense from a mathematical perspective, it isn't as relevant when it comes to programming.
Why does the indexing start with zero in 'C'? - Stackoverflow (opens new window)
しかし Python は数学的な一貫性を大事にしている気配があります。
例えば関数を定義するときに使う予約語は def です。
これは数学の定義を示す時に使われる語と同じです。
# 4.3. まとめ
以上のことから
b の 0 <= i < n が数字の範囲を表すときには良い表現だと言えます。
こういうのを難しい言葉で「左閉右開の半開区間」と言います。
C 言語で n 個の数字の並びを表すときに、 次のように表現することがあります。
// n 回処理を繰り返す
for(i = 0; i < n; i++){
...
}
// n 回処理を繰り返す
for(i = 1; i <= n-1; i++){
...
}
いま見てみると for 文を1度も回さないときには n = 0 を代入すれば良いですし、n 回繰り返すときも綺麗に表現できるので、 こうしてみるととても綺麗な表現に見えます。
なぜ上の方が綺麗かというと、 下の書き方の場合 n に 0 を代入してしまうと i <= n - 1 で 自然数でない値 -1 が登場してしまいます。
# 5. アドレス空間の観点から
答え: メモリアドレスの参照について考えたときに色々とあたりがあるから。
これについては以下を参考にして書きました。
- Why does the indexing start with zero in 'C'? - Stackoverflow (opens new window)
- Why The Array Index Should Start From 0 (opens new window)
おそらくこれは直接 Python とは関係がないように感じます。 なぜなら メモリ も アドレス も Python には関係ないからです。 ただ比較的よく引き合いに出される説明なので、簡単にご紹介させていただきます。
コンピュータは、内部的には 0 と 1 の数字の羅列でデータを保存しています。 データを保存する範囲を メモリ と言います。 メモリには 0 と 1 を保存する小さな箱が連なっています。 その 0 と 1 を保存する各箱には アドレス という番号が振られています。 0 と 1 の数字のことを総称して ビット と言います。
# 5.1. 問題
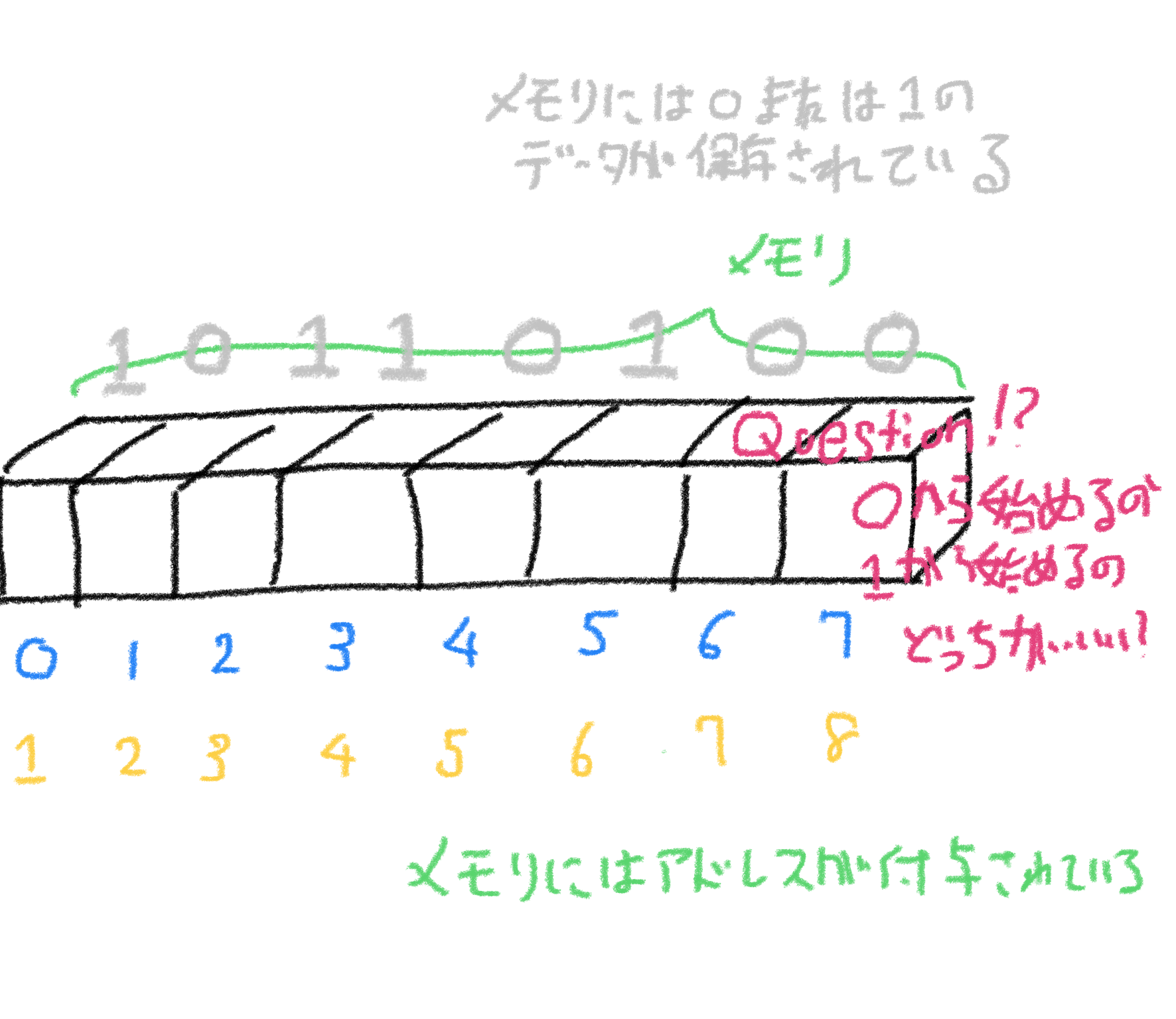
アドレスを 0 からはじめた場合、すべてのメモリのすべての箱を参照できるようにするには 何 bit 必要ですか? また、アドレスを 1 からはじめた場合、メモリのすべてのアドレスを参照できるようにするには 何 bit 必要ですか?
# 5.2. 回答
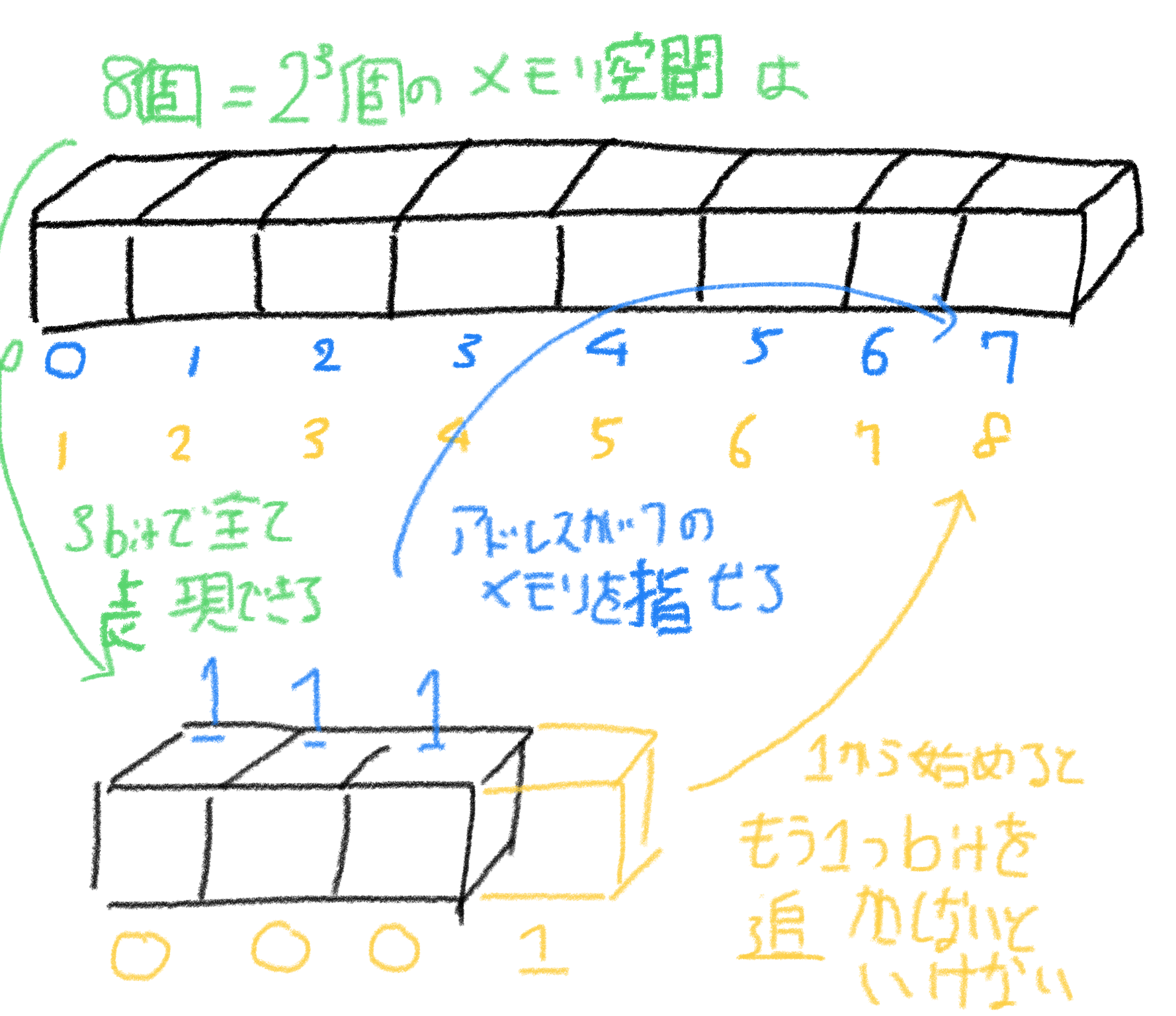
2^n bit のメモリ空間は、n bit のメモリ空間があれば参照可能です。 例えば 8 bit, 2^3 bit のメモリ空間は、3 bit のメモリ空間があれば参照が可能です。
しかし、これを 1 からはじめてしまうと 4 bit 必要になってしまいます。 半分のメモリ空間が不要になってしまいます。
具体的にどこに問題が生じるのかは、自分は正直理解していません。 低レイヤでアドレスの変換をするコードを書くよりは、 上位側で低レイヤを意識して 0 からはじめた方が、このケースでは良いような気がします。
結論 (opens new window)
0 から数え上げると決めたことは、 下位のシステムが解釈できるようにコードを変換することを簡単にするため そのデジタルシステムの上で走っているソフトウェアも含めた、すべてのデジタルシステムで長く浸透している。 もしそうでなければ機械とプログラマの間で、メモリの参照ごとに不必要な変換が必要になっていたでしょう。 0 から数え上げることはコンパイルを簡単にします。Conclusion
The decision to start count at 0, has since permeated all digital systems, including the software running on them, because it makes it simpler for the code to translate to what the underlying system can interpret. If it weren't so, there would be one unnecessary translation operation between the machine and programmer, for every array access. It makes compilation easier.
コンピュータサイエンス的な背景を考えれば、 インデックスを 1 からはじめてしまうことは、 C言語などより低レイヤーに移ったときに今後の理解を妨げることになります。
このことを踏まえると Python も 低レイヤー向けの言語と合わせて 0 からはじめることが、望ましいように感じます。 実際に議論したメールがあれば欲しい...
# 5.3. まとめ
以上、未満であれば 0 からはじまる空の範囲 range を自然数で表現できます。 また 0 からはじめた方が、 将来的なコンピュータサイエンスの理解につながりそうです。
# 6. 他言語では
他言語では、どう表現されているのでしょうか?
# 6.1. 大枠では
0 から n - 1 までが多数派です。 最近生まれた言語だと例外的に Julia と Nim が 1 から n になっています。
- Comparison of programming languages (array) - Wikipedia (opens new window)
- 0と1、どちらから数えるか - ありえるえりあ (opens new window)
- 配列のインデックスは0,1,どちらから始まる方が良い? - Qiita (opens new window)
こちらのツイートから知ることができました。ありがとうございます。
それぞれの言語と配列の最初のインデックス値の比較。awk, julia, lua, smalltalk などが1始まりの仕様になっている。 https://t.co/Tg3gEuqOHy
— Tetsuya Morimoto (@t2y) May 2, 2019
歴史的経緯だとすべてのビットがゼロの値を無駄にしたくないという背景らしい。配列が連続したメモリ領域で offset の演算に便利だったというのはいまでも通じるところかな https://t.co/ixt4MaNAot
— Tetsuya Morimoto (@t2y) May 2, 2019
# 6.2. Kotlin の Range 式
Kotlin には Range 式という表記があるそうです。
例えば 1, 2, 3, 4 を 1..4 と表記できます。
fun main() {
for (i in 1..4) print(i)
}
Range 式は rangeTo 関数 (opens new window) によって形成されます、 Range 式で形成されたオブジェクトは
inまたはin!で補完される..という形式の演算子を持っています。 Range は、すべての比較可能な型のために設計されましたが、 integral primitive な型には、それに最適化した実装がなされています。 以下、いくつか range の使い方を示した例があります:
Range expressions are formed with rangeTo functions that have the operator form..which is complemented byinand!in. Range is defined for any comparable type, but for integral primitive types it has an optimized implementation. Here are some examples of using ranges:
Ranges - Kotlin (opens new window)
ちなみに Python の昔のメーリングリストを漁っていた時にこの記法が提案されて、 Guido が却下してるのをどこかで見かけました。 Guido はかなり年月を置いてから承認するということをするのですが、 この記法についてはしませんでした。
Python は、特殊な記法を嫌います。
特殊なケースは一貫性を破るほど特殊ではない。
Special cases aren't special enough to break the rules.
The Zen of Python - PEP 20 (opens new window)
Python の世界では、文法は大抵の場合、最終手段です。 コンパイラの助けなしに解決できないような場合に使います。
Within Python's world, syntax is generally used as a last resort, when something can't be done without help from the compiler.
Make print a function - PEP 3105 (opens new window)
# 7. まとめ
ここまで以下のように見てきました。
Python は初学者にも理解しやすい設計をされているような気がしました。 その中で range を「以上」、「未満」で表現しているのは、 わかりにくくなぜこのようにしているのか長いこと疑問でした。
Python ではアドレスを意識することはほぼないので、 おそらく「アドレス空間 (opens new window)」よりも「数学」的な一貫性の観点から、 「以上」、「未満」を採用したのではないかなと思ったりします。
Guido は range を文字どおり範囲を表現することを意図していたのかなと思います。
すると Dykstra が説明してくれたとおり範囲を表現するには
「以上」、「未満」の方が都合がいいからです。
