
# Python でアルゴリズム
速くなります
# はじめに
アルゴリズムと聞くと難しそうですが、 「はんぶんこにすると速くなる」 という雰囲気が伝わればと思いました。これだけです。 頑張ってコードを書きましたが、 個々の細かいコードは、あまり掘り下げなくてもいいかなと感じたりもします。
# Why? - なんのために勉強するの?
# (1) 速くなることがあることを知るため
アルゴリズムを書き換えるとメチャクチャ速くなることがあります。 そのことを知る意味ではソートは、一番簡単な例の様に思えます。 業務系のコードを書く中で、これを知る自分自身で体系的に知り得るということは、 かなり稀なんじゃないかなと思ったりします。
つまり、10万ユーザあたり1台必要なら、100万ユーザで10台、1000万ユーザで100台、1億ユーザで1000台と、規模に正比例して台数が増えていくことになります。(実際には並列化によるオーバーヘッドでさらに悪化していきます) ... 中略 ...
10万ユーザあたり1台なら、100万ユーザで2台、1000万ユーザで3台、1億ユーザで4台というように、対数的にしか増えていかないようにする、 これがアルゴリズムの本当のパワーです。
MongoDBの様なNoSQLに勢いがあるのは何故ですか?SQLと比べてどんな利点や欠点がありますか? (opens new window)
ここでお伝えしたいことは「速いコードを書くこと」ではないです。 「速くなることがあることを知ること」です。 初めてアルゴリズムを習った時に、 プログラミングスキルを向上させるために、 ソートのアルゴリズムを勉強するのだと思いました。
でも、実際にソートのアルゴリズムを勉強したくらいでは、向上しないなと思いました。 既にソートのアルゴリズムを学習された方から言わせれば、 お前はなにを言っているんだ?という感じですが笑 肩の力を抜いてやっていけばいいかなと思っています。
やっぱり凄い方がたくさんいます。 そして、速いコードを書くためにアルゴリズムを勉強される方がいます。 正直、私の能力を完全に超えているので、 どうやって速いコードを書くためにアルゴリズムを学習するのかという観点では、書けていません。 あくまでもこのページの目的は、アルゴリズムに触れることだけです。
中国の競プロ事情を聞いてみたら、「競プロで高校生best50に入ったらその時点で大学選び放題」って話を聞いて、そのための専門塾みたいなのも存在するらしくって、10歳くらいから競プロをするのが普通、という感じらしく、そりゃ強いわと思うし、よく日本これだけ戦えてるなあって気分になった。
— chokudai(高橋 直大)🍆🍡 (@chokudai) December 5, 2019
# (2) コードを書く練習のため
コードを書くとき、どうされていますか? まず頭の中に「データの流れ」があって、 次にそのデータの流れを「コード」に書き込んでいるのではないかなと思います。


if 文, for 文といった制御構造、 あるいはリスト, 辞書といったデータ構造を習っただけでは、 どうしてもコードは書けないところがあります。 そうすると、実際にコードを書いて練習していく必要があります。
コードを書く練習をしてもらう時に一番大変だなと思うことは、 完璧は無理でも将来それなりに役に立ってくれるかもしれない題材を設定することです。 「アルゴリズム」は、典型的な「データの流れ」が、 とても簡潔にまとまった、圧倒的に質の高い題材です。
アルゴリズムを習ったからといって、必ずしも実務に役立つわけではないと思います。 しかし、コードを書いて練習しないといけないですよね、 となった時には、アルゴリズムは最適な題材だと個人的に思っています。
逆に言えば、既に実務でそれなりにゴリゴリ書かれている方の場合、 コードを書く練習をするために ソートのアルゴリズムを習ったとしても効果が薄いかなと思います。
その辺が「アルゴリズムを勉強することには意味がない」けど、 なぜか科目として取り上げられているということにつながっているのかなと思ったり、思わなかったりします。
# What? - なにを勉強すればいいの?
どのくらいの範囲のものを勉強するべきでしょうか?
「アルゴリズム」という言葉があって何を意識して、 学べばいいのか分からないと言うのがあるのかなと思います。
出題範囲が無限にあるのかなと思うと気が遠くなります。 まずは、基本情報技術者試験の出題範囲を基準にして学習すればいいかなと思います。
千尋。エンジニアになりたいなら、まず基本情報技術者試験を受けよう。
— じゃすてぃん校長@tech boost (@justin_tb_) August 16, 2019
これに受かれば君も一歩エンジニアに近づける。
参考書は、この『キタミ式』がイラスト解説で分かりやすくてオススメだ。
たくさん勉強して、エンジニアになって、いつか私と一緒にサービスをリリースしよう。 pic.twitter.com/uWKyKUkQbV
栢木先生のほかに、キタミ式も有名らしいです。 基本情報技術者試験の参考書を買う必要性は全くないですが。 ただ、上のツイートの画像が面白かったので掲載しました笑
まず、データ構造。
- 配列
- リスト
- キュー
- スタック
- 二分探索木
- 二分ヒープ
そして、次にアルゴリズム。
- バブルソート
- 選択ソート
- 挿入ソート
- シェルソート
- クイックソート
- ヒープソート
- マージーソート
- 線形探索法
- 二分探索法
本当にそうなの?って感じですが。 書籍や Udemy のアルゴリズムの入門書などの目次を見てください。 よくよく見ると、ボリュームの大小はありますが、 だいたい上記で列挙したアルゴリズムとデータ構造が共通で取り扱われているのがわかります。
アルゴリズムの入り口は、決まりはないものの共通認識があり、 比較的、決まった様な題材が取り上げられている気がします。 やらないといけないことが無限大にあると思うと、やる気が削がれます。 入り口部分については、そんなことないですよ、という、そんな感じです。
# How? - どうやって勉強すればいいの?
良い時代になったもので、優れた書籍や Udemy の講座が多数あります。 例えば、素晴らしい書籍や Udemy の講座が多数あります。
ただ、いきなり Python のコード 書こうとしたり、あるいは 計算量の話 を聞いてしまうと、負荷が高く、辛い思いをされたりするのかなと思ったり、思わなかったりします。
ポイントはアルゴリズムという「全体」から、 少しずつ Python のコードという「詳細」に落としていくことだと思っています。
- 動画を見る
- アプリで手を動かす
- コードを書く
# Step 1. 動画を見る
YouTube の動画がとてもわかりやすいです。 まず YouTube でアルゴリズムの雰囲気を把握します。 理解する必要はないです。
# 線形探索
# 二分探索
# バブルソート
# 挿入ソート
# ヒープソート
# マージソート
# クイックソート
# ダイクストラ(本サイトでは扱わないけどわかりやすい)
# A*アルゴリズム(本サイトでは扱わないけどわかりやすい)
# Step 2. アプリで手を動かす
次に「アルゴリズム図鑑」の「実験モード」を使って、 手を動かしてアルゴリズムを確認します。
個人的にクオリティが高いと感じています。 2016年 App Store「今年のベストApp 10選」に選出され、 2017年4月の段階で50万ダウンロード達成したそうです。
また iPhone はわからないのですが Android は 370 円のアプリ内課金のみ で全アルゴリズムを学習できます。 書籍や Udemy に比べると圧倒的に安く、 万が一、合わなかったとしても、 そこまで痛い出費ではないかなと思います。
視覚的にアルゴリズムを学べるiPhone/Androidアプリ「アルゴリズム図鑑」めちゃいい。
— Hideto🇨🇦エンジニア海外就職の応援団長 (@VancouBoys) July 15, 2019
プログラミング学習は視覚的でない部分が多いので理解が難しいけど、 こんな感じでイラストとアニメーションでイメージできると理解のスピードが段違いだと思う。 pic.twitter.com/OhW1dHzSGH
日本語版もあります。 題材として取り上げられているものは、基本情報技術者試験などで使われる一般的なアルゴリズムのみで、 重箱の隅をつつくようなアルゴリズムはありませんでした。
# Step 3. コードを書く
Step 1, 2 を通して「データの流れ」の部分が出来上がりました。


ここからは Step 3 の「コードを書く」段階です。 書籍、あるいは Udemy からご自身の肌に合いそうなものを選び、 実際にコードを書く練習するのがいいのかなと思います。
| 媒体 | Udemy | Udemy | 書籍 | 書籍 | 書籍 | 書籍 |
| 発刊 | 2019 11 | 2019 11 | 2019 11/26 | 2020 01/11 | 2020 01/24 | 2018 06/30 |
| 価格 | 5400 | 5400 | 2400 | 2640 | 2200 | 2400 |
# カリキュラム
ここからは広告です。 このサイトではどうやって取り扱うかを書いていきます。 このサイトでは、まず「探索」から始まり「木」、 そして「ソート」に話を持っていきます。
# (1) 探索

最初に「二分探索」を持って来たのは、比較的簡単だからです。 また、そのあとの「二分探索 木 」につなげることができるからです。
二分探索では、標準ライブラリ bisect (opens new window) を取り上げます。 ソースコードである bisect.py (opens new window) は短く、取り掛かりやすい気がします。 標準ライブラリに慣れることも、このページの目的です。
# (2) 木


残念ながら、木には動画がありません。 「アルゴリズム図鑑」で学習されていることを想定しています。 代わりに木をコンソールに表示するツールを作りました。 これで動作確認が楽になるはずです。
bst = BinarySearchTree(BinarySearchNode)
bst.insert(8)
bst.insert(3)
bst.insert(1)
bst.insert(6)
bst.insert(10)
bst.insert(4)
bst.insert(7)
bst.insert(14)
bst.insert(13)
print(bst)
>>> print(bst)
08
03 10
01 06 14
04 07 13
>>>
木は見ると難しそうなのですが、やっていることはとても単純です。 二分探索木は左右に、二分ヒープは上下にデータを分けています。
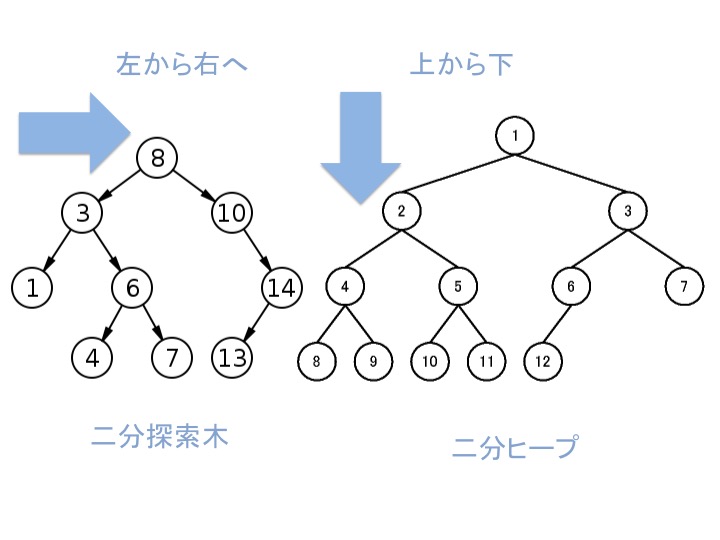
「二分ヒープ」では標準ライブラリ heapq (opens new window) を題材に取り上げます。 ソースコードである heapq.py (opens new window) は開くとウワッって感じがするのですが、やっていることそのものはとても単純です。
# (3) ソート
最後に「マージソート」と「挿入ソート」、「クイックソート」、「ヒープソート」について触れていきます。 「バブルソート」を改良すると挿入ソートになるので、バブルソートについて触れてから挿入ソートに話を持って行っています。
最終的に Python で使われているソートアルゴリズム TimSort に関する以下の記事の雰囲気が伝わればと思っています。 自分も外面しかまだ読めてません。 ここで前提とされている知識、クイックソート、マージソート、ヒープソート、挿入ソートには触れて、 なんとか興味が持てるくらいのラインにまでいければと考えています。
高速な安定ソートアルゴリズム TimSort の解説 (opens new window)
しかしながら、オリジナルのTimSortのコードは若干複雑で、 実際のところどういうアルゴリズムなのかわかりづらいところがあると思います。
そこで今回はTimSortのアルゴリズムをできるだけわかりやすく解説してみたいと思います ( クイックソート、マージソート、ヒープソート、挿入ソート の知識を前提とします)。
# (4) 素数
素数はおまけです。
「素数」については、力技で調べざるを得ないので、 あまり得るものはないかなという感じもします。 純粋にコードの書き方の世界という感じがします。
たまに競プロででてきたりするので、 雰囲気だけ押さえておけばいいかなとも思います。
# おわりに
ここまで以下のように見てきました。
なんで速くなるのでしょうか? それは「はんぶんこ」にして、比較回数が少なくしているからです。 いまはパッと説明が思いつかないのですが。 いつか、アニメーションにして説明して見たいと思います。
ソートや二分探索木の話は「はんぶんこにしたら速くなる」。 これだけ押さえておけばいいかなと思います。 巷の書店で売っているアルゴリズムのコードとかを読むときもそれでいいんじゃないかなと。
この「はんぶんこ」アルゴリズムを難しい言葉で「分割統治法」と言います。 なんでこんなに難しい言葉になってしまったのでしょうか笑
主に分割統治法に焦点を当てて話を進めていきます。 はんぶんこにしたら速くなることです。 細かいコードは掘り下げなくて大丈夫です。