Last Updated: 2/6/2024, 5:44:57 AM

# 二分ヒープ

# 1. ヒープとは

ヒープ（英: heap）とは、「子要素は親要素より常に大きいか等しい（または常に小さいか等しい）」という制約を持つ木構造の事。単に「ヒープ」という場合、二分木を使った二分ヒープを指すことが多いため、そちらを参照すること。
ヒープ -Wikipedia (opens new window)

スライドに概要をまとめました。

heapq の概要

speaker deck

# ◯ 応用

# ヒープソート

ヒープには、下より上の要素が小さいという制約があります。そのため１つずつ一番上から取り出すとソートすることができます。これをヒープソートと言います。

ここで神のごとくわかりやすい、わくわくアカデミーの動画を引用させていただきます。動画を見ると、だいたいの雰囲気が掴みやすいかなと思います。

# 優先度付きキュー

こんなものそもそもどこで使うんだ？という話です。正直、あまり理解していません。

人間は様々なお仕事を抱えています。お仕事には、それぞれに優先度がありますし、基本的には優先度の高いお仕事から、片付けていきます。

片付けつつも、途中で、新しいお仕事が振り込まれます。新しいお仕事の優先度が高ければ上に置きたいですし、低ければ下に置きたいです。そんなときに使うものらしいです。

このようなものを優先度付きキューと言うらしいです。ヒープは、優先度付きキューの実装のうちのひとつです。 Wikipedia によると優先度付きキューの実装として、ヒープが実装されることが多いらしいです。

Java
java.util.PriorityQueue が標準クラスライブラリにあり、二分ヒープで実装されている。
優先度付きキュー - Wikipedia (opens new window)

# ◯ データ構造

実際には木にはせず、リストで代用します。こういうのは作りません。

class Node:
    value: int
    left: Node
    right: Node

なぜかというと要素を追加するときに、最後の位置を求めるのが面倒だからだと思っています。

例えば、木構造にしたときに要素を追加する挙動をどうやって実装したらいいでしょうか？言い換えれば、どうやって最後の位置を特定すればいいでしょうか？

要素の数を記録させておけばできないこともないと思うのですが、ちょっと面倒な感じになりそうです。

リストを代用すれば、リストの末尾に append するだけで解決できてしまいます。

# 2. サンプルコード

とりあえず触って動作を確認して見たいと思います。 heapq (opens new window) というリストをヒープにしてしまう標準ライブラリがあるので、これを使います。

標準ライブラリというのは pip install したり git clone しなくても最初から import できるパッケージやモジュールを指しています。

ただ、リストのまま表示しても、とっかかり辛いかなと感じたので、リストから print できる二分木を生成する BinaryHeap というクラスを作りました。

$ git clone https://github.com/niconico25/tree
$ cd tree
$ python3  # Python の対話モードを開く

# 対話モード >>> に
# コピペで実行できます。
from heapq import heappush
from heapq import heappop
from heapq import heapify
from tree.binary_heap import BinaryHeap


#
# 1) 単純に並べただけで
#    まだヒープではない。
#
lst = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
print(BinaryHeap(lst))
#               01              
#       03              05      
#   07      09      02      04  
# 06  08  00      

#
# 2) heapify 関数でヒープにする。
#    上が大きく下が小さいです。
#
heapify(lst)
print(BinaryHeap(lst))
#               00              
#       01              02      
#   06      03      05      04  
# 07  08  09  


#
# 3) heappop
#
heappop(lst)
# 0

print(BinaryHeap(lst))
#               01              
#       03              02      
#   06      09      05      04  
# 07  08      

heappop(lst)
# 1

print(BinaryHeap(lst))
#               02              
#       03              04      
#   06      09      05      08  
# 07  

heappop(lst)
# 2

print(BinaryHeap(lst))
#       03      
#   06      04  
# 07  09  05  08


#
# 4) heappop
#
heappush(lst, 10)
print(BinaryHeap(lst))
#               03              
#       06              04      
#   07      09      05      08  
# 10   

heappush(lst, 1)
print(BinaryHeap(lst))
#               01              
#       03              04      
#   06      09      05      08  
# 10  07

# 3. 操作の概要

ヒープをリストで表現します。標準ライブラリ heapq (opens new window) のコードを読みたいと思います。

# ◯ heapq のコードの場所

特殊属性 __file__ か、あるいは GitHub からも確認できます。

# 1) file

対話モード >>> を開いて __file__ を確認すればわかります。

>>> import heapq
>>> heapq.__file__
'/usr/local/Cellar/python/3.7.2_2/Frameworks/Python.framework/Versions/3.7/lib/python3.7/heapq.py'
>>>

# 2) GitHub

あるいは GitHub からも見ることができます。

python/cpython/Lib/heapq.py - GitHub (opens new window)

# ◯ 本当は...

実際に import heapq したときは C 言語で実装されたものが使われています。ここでは Python での実装を見ていきたいと思います。

# If available, use C implementation
try:
    from _heapq import *
except ImportError:
    pass

heapq.py #L585-L589

# ◯ 実際に見る関数

heapq.py を開くと、たくさんの関数が書かれていますが、ここで必要なのは以下の５つの関数だけです。しかもすべて足し合わせても 6, 70 行程度ととても短いです。

1, 2, 3, 4 に比べると 5 の heapify 関数はすこし混みいっています。

heappush
_shiftdown
heappop
_shiftup
heapify

# 1. heappush 関数

# 1.1. 概要

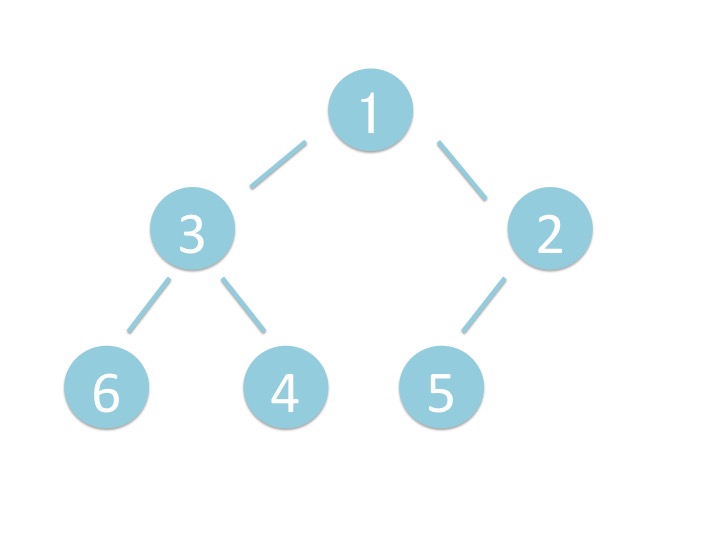
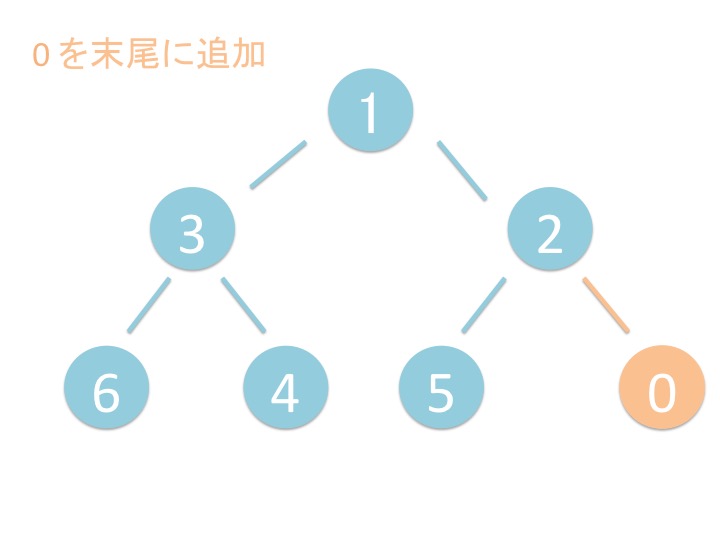
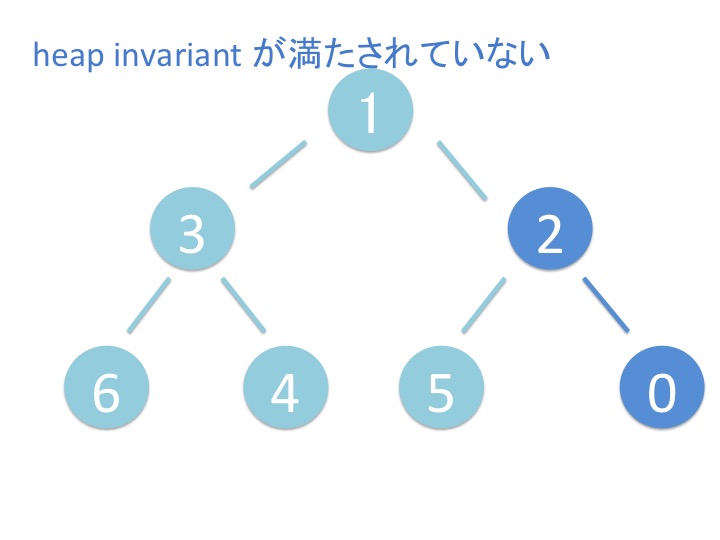
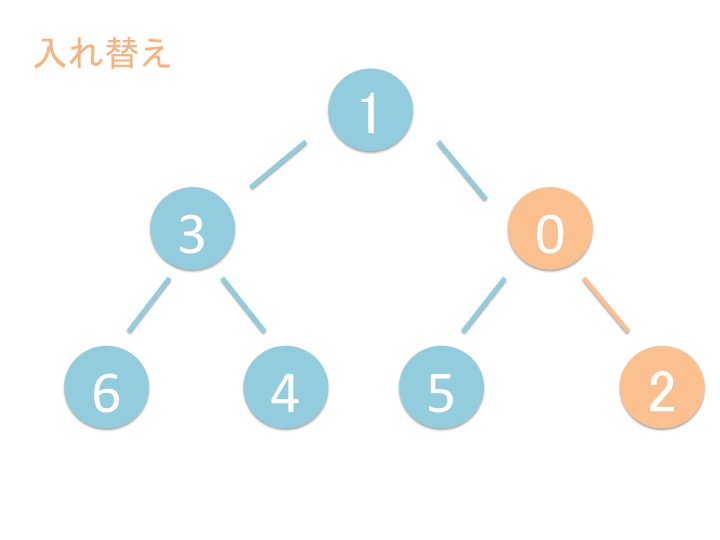
heappush(heap, item) 関数はヒープ heap の葉に新しい要素 item を追加して、要素を上に持ち上げていきます。

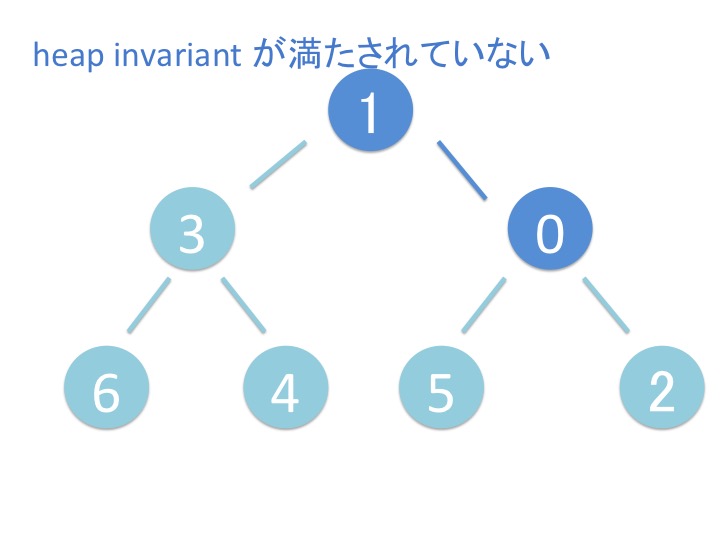
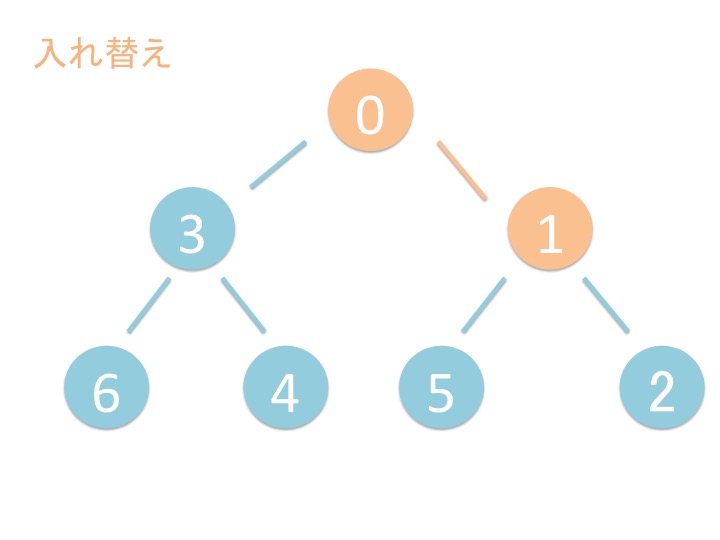
# 1.2. さわってみよう

heappush の途中結果を出力するものを用意しました。これを実行してみていただいた方が早いかなと思います。

$ git clone https://github.com/niconico25/tree
$ cd tree
$ python3  # Python の対話モードを開く

# 対話モード >>> に
# コピペで実行できます。
from heapq import heappush
from tree.binary_heap.heapq import heappush as heappush_print

heap = [] 
heappush(heap, 6)
heappush(heap, 5)
heappush(heap, 4)
heappush(heap, 3)
heappush(heap, 2)
heappush(heap, 1)
heappush_print(heap, 0)

>>> heappush_print(heap, 0)

heappush
      01      
  03      02  
06  04  05    

_shiftdown 0 -> 1 要素 0 から 1 に向けてバブルアップ
_shiftdown: before
      01      
  03      02  
06  04  05  00
_shiftdown: in progress
      01      
  03      02  
06  04  05  02
_shiftdown: in progress
      01      
  03      01  
06  04  05  02
_shiftdown: after
      00      
  03      01  
06  04  05  02
>>>

# 1.3. ソースコード

_siftdown 関数に startpos, pos という引数があります。 heappush は葉から根までたどるだけなので、この引数が必要なのか、疑問だったのですが、この引数は heapify 関数で使います。

def heappush(heap, item):
    # 1) 末尾に追加して
    heap.append(item)
    # 2) 上にバブルアップさせる。
    _siftdown(heap, 0, len(heap)-1)

def _siftdown(heap, startpos, pos):
    newitem = heap[pos]
    while pos > startpos:
        parentpos = (pos - 1) >> 1
        parent = heap[parentpos]
        if newitem < parent:
            heap[pos] = parent
            pos = parentpos
            continue
        break

    heap[pos] = newitem

# 2. heappop 関数

# 2.1. 概要

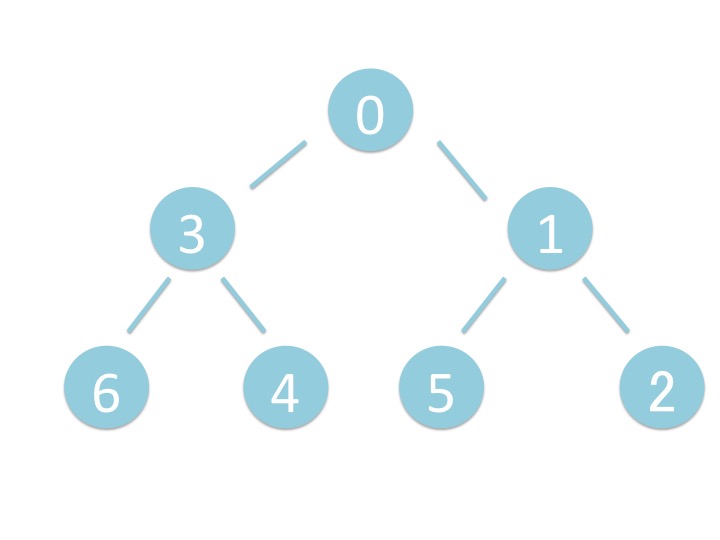
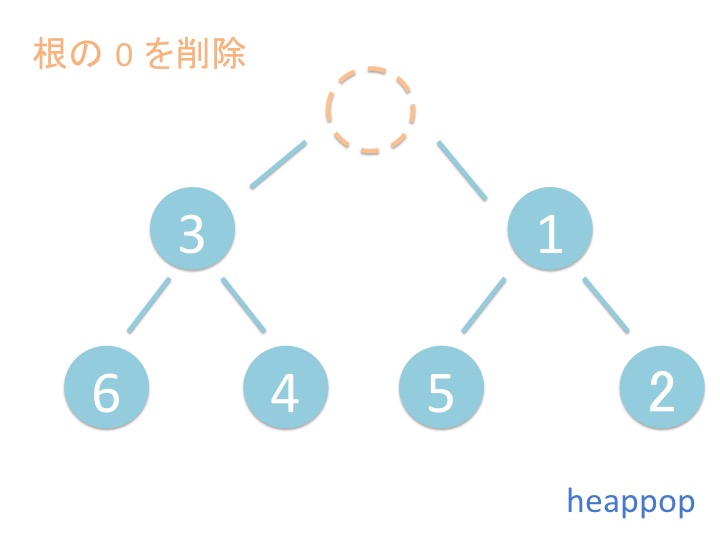
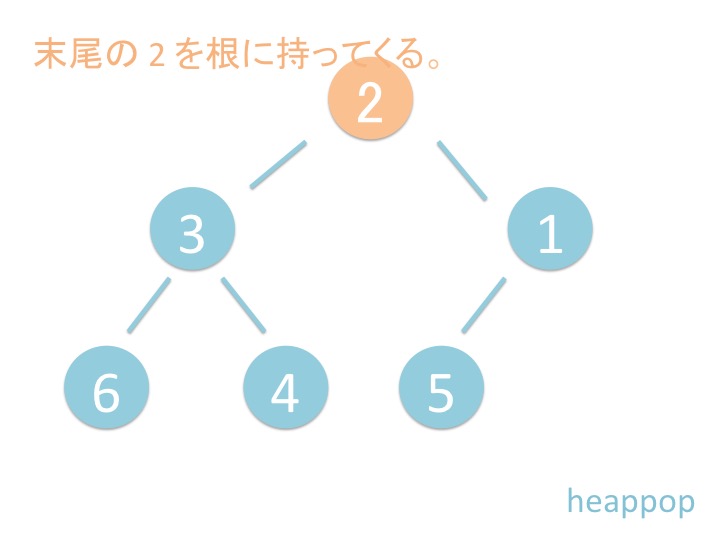
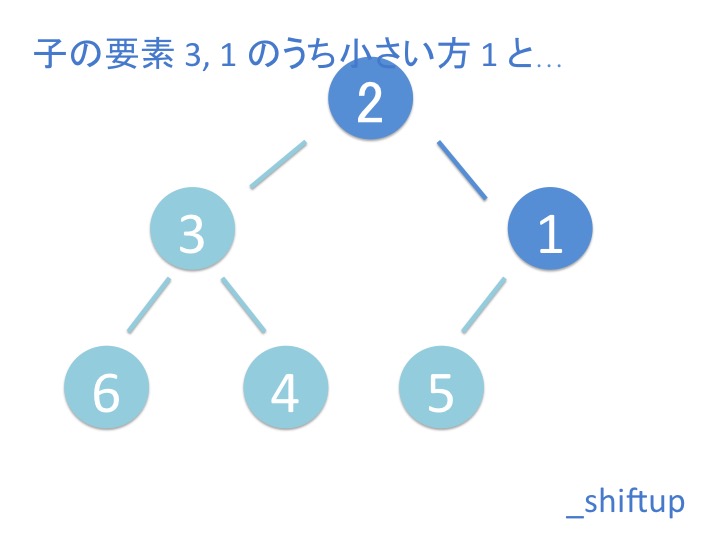
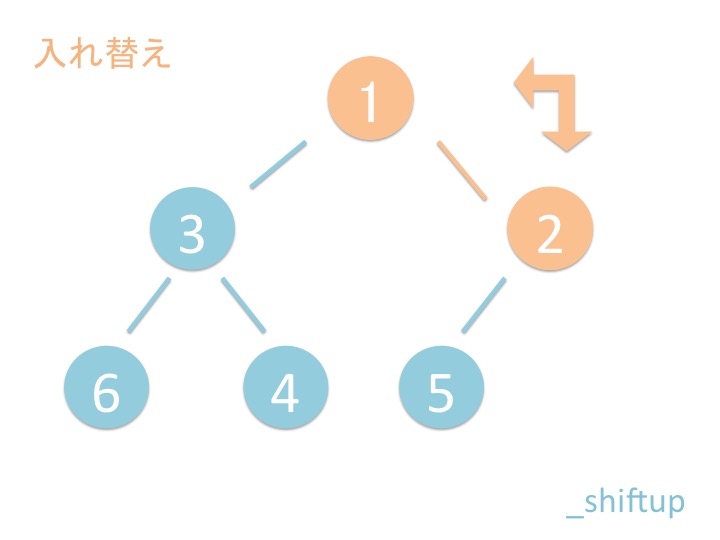
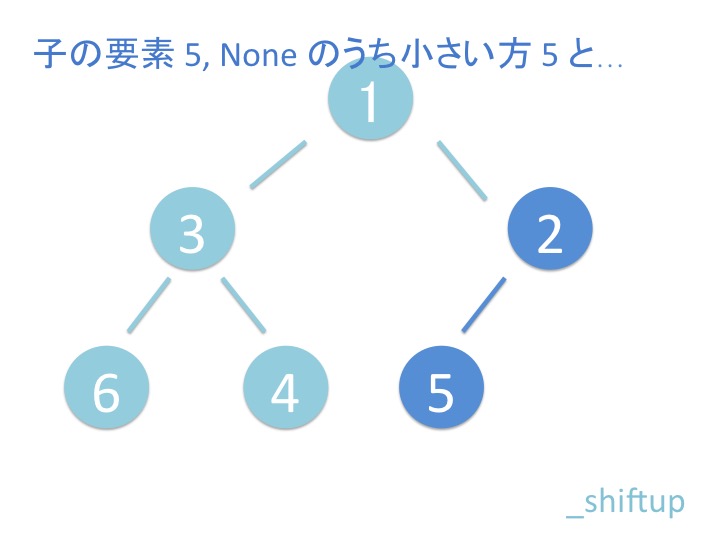
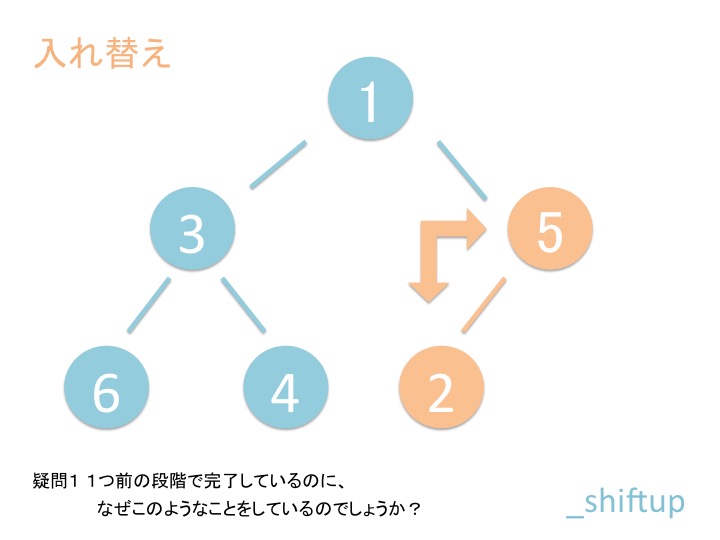
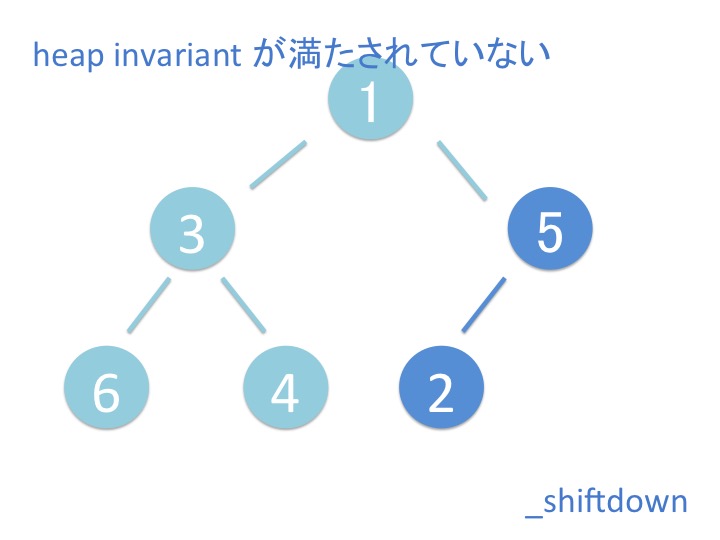
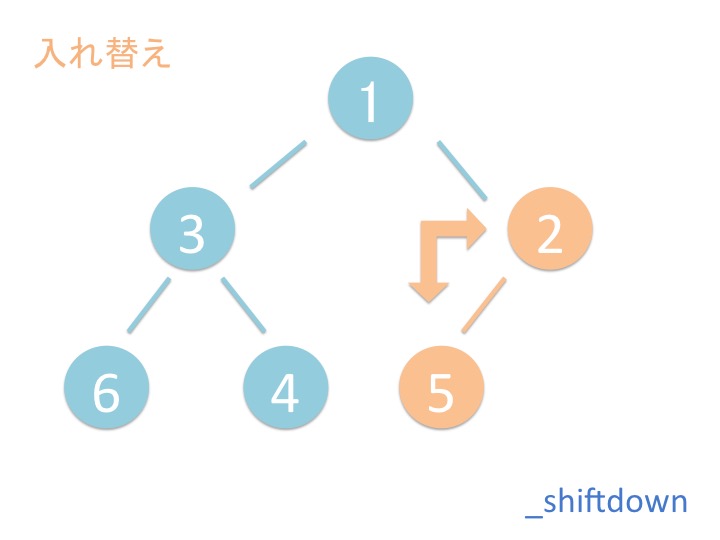
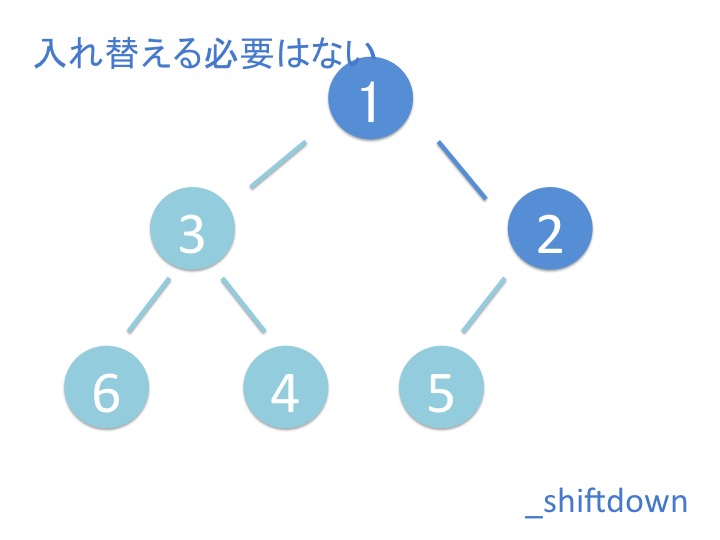
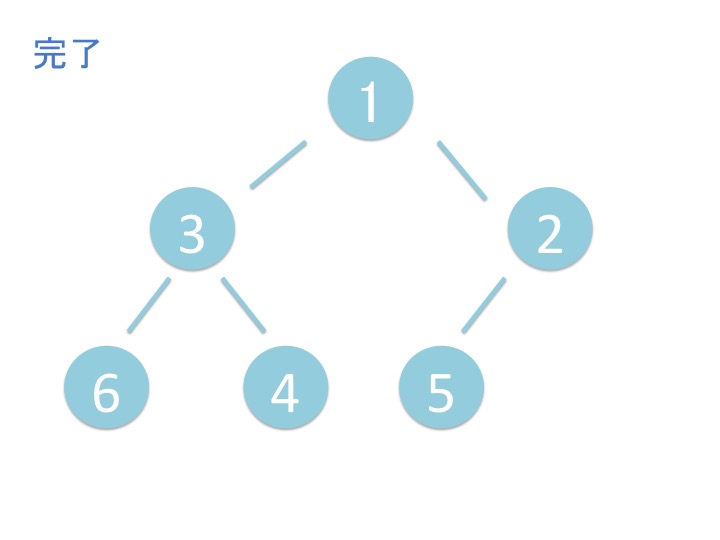
上から下にバブルダウンするだけではなく、折り返してまた上に来ています。これはどういうことでしょうか？

途中で break するのは最後の方になるから、とりあえず問答無用で一番下まで行ってそれから折り返してしまう方が効率がいいらしいです。

heapq.py のソースコードにコメントがあったのでご紹介します。

私たちは親が２つの子よりも小さい場所を見つけたらすぐにループを抜けることが できます、しかし、これは悪いアイディアです、多くのアルゴリズムの本でそのように書かれてはいるのですが。
We could break out of the loop as soon as we find a pos where newitem <= both its children, but turns out that's not a good idea, and despite that many books write the algorithm that way.

heap pop をしている間、最後の配列の要素は根に移動してきます、そしてその要素の値は大きくなる傾向があります、そのため根から始まる一連の値と比較しても、大抵効果がありません（= 大抵の場合、ループから早く抜け出させてはくれません） Knuth の第 3 巻を参照してください、演習の中で、このことが説明され定量化されています。
During a heap pop, the last array element is sifted in, and that tends to be large, so that comparing it against values starting from the root usually doesn't pay (= usually doesn't get us out of the loop early). See Knuth, Volume 3, where this is explained and quantified in an exercise.

# 2.2. さわってみよう

heappop の途中結果を出力するものを用意しました。これを実行してみていただいた方が早いかなと思います。

$ git clone https://github.com/niconico25/tree
$ cd tree
$ python3  # Python の対話モードを開く

# 対話モード >>> に
# コピペで実行できます。
from heapq import heappush
from tree.binary_heap.heapq import heappop as heappop_print

heap = [] 
heappush(heap, 6)
heappush(heap, 5)
heappush(heap, 4)
heappush(heap, 3)
heappush(heap, 2)
heappush(heap, 1)
heappush(heap, 0)
heappop_print(heap)

>>> heappop_print(heap)

heappop
      00      
  03      01  
06  04  05  02

_shiftup 2 -> leaf 要素 2 から葉に向けてバブルダウン
_shiftup: before
      02      
  03      01  
06  04  05    
_shiftup: in progress
      01      
  03      01  
06  04  05    
_shiftup: in progress
      01      
  03      05  
06  04  05    
_shiftup: after
      01      
  03      05  
06  04  02    

_shiftdown 2 -> 1 要素 2 から 1 に向けてバブルアップ
_shiftdown: before
      01      
  03      05  
06  04  02    
_shiftdown: in progress
      01      
  03      05  
06  04  05    
_shiftdown: after
      01      
  03      02  
06  04  05    
0
>>>

# 2.3. ソースコード

ここで押さえておきたいことは次の２点だけです。

まず _shiftup 関数を呼び出し、最後に shiftdown 関数が呼び出されています。 _shiftup で葉までたどり着いた後に、shiftdown 関数で根に向けて登っていきます。

また _shiftup 関数の中では break 文がありません。これは _shiftdown 関数の中に break 文があったことと対照的です。

def heappop(heap):
    """Pop the smallest item off the heap, maintaining the heap invariant."""
    lastelt = heap.pop()    # raises appropriate IndexError if heap is empty
    if heap:
        returnitem = heap[0]
        heap[0] = lastelt
        _siftup(heap, 0)
        return returnitem
    return lastelt

def _siftup(heap, pos):
    endpos = len(heap)
    startpos = pos
    newitem = heap[pos]
    # Bubble up the smaller child until hitting a leaf.
    childpos = 2*pos + 1    # leftmost child position
    while childpos < endpos:
        # Set childpos to index of smaller child.
        rightpos = childpos + 1
        if rightpos < endpos and not heap[childpos] < heap[rightpos]:
            childpos = rightpos
        # Move the smaller child up.
        heap[pos] = heap[childpos]
        pos = childpos
        childpos = 2*pos + 1
    # The leaf at pos is empty now.  Put newitem there, and bubble it up
    # to its final resting place (by sifting its parents down).
    heap[pos] = newitem
    _siftdown(heap, startpos, pos)

この折り返すやり方、最初は、えー本当なの？って思ってたのですが... Java や Python で採用されているソートアルゴリズム TimSort の作者である Tim Peter 氏が実装に関わっているらしいので、確かだと思います。きっと。

# 3. heapify 関数

# 3.1. 概要

末尾から _shiftup を実行するだけです。

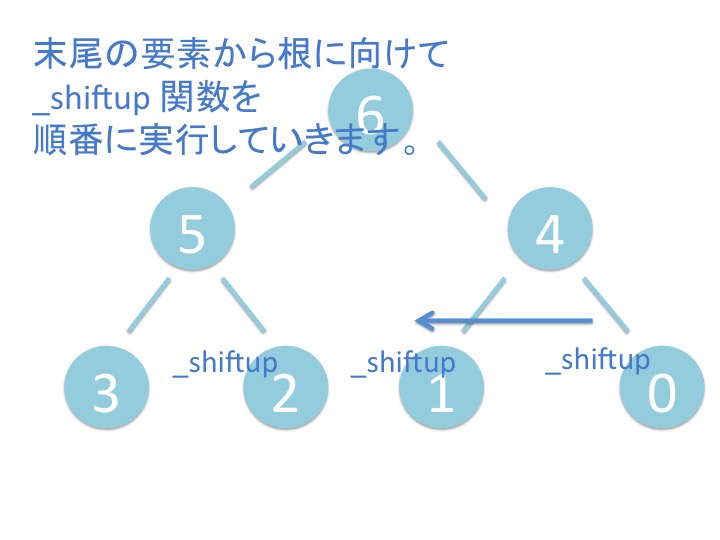
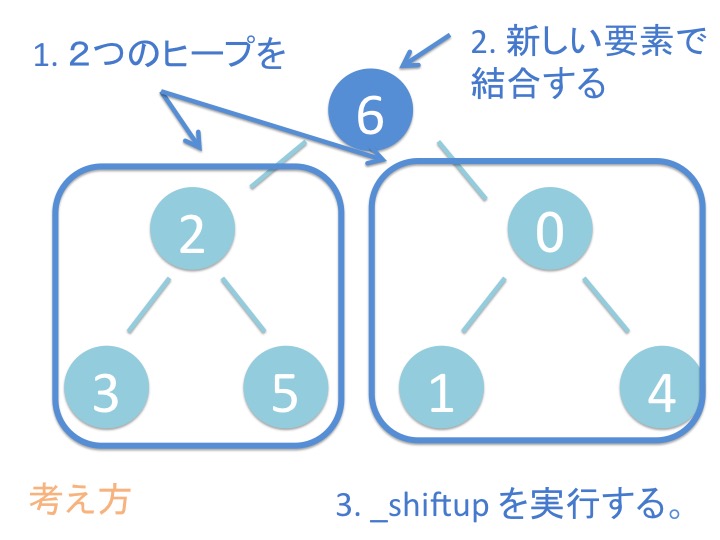
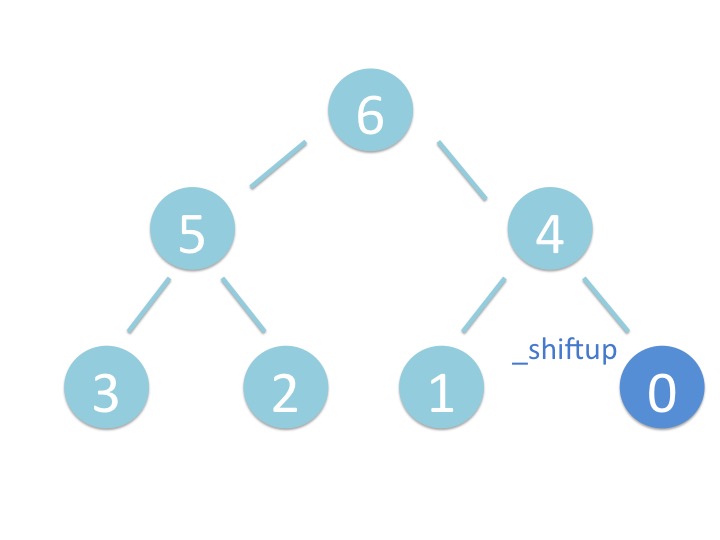
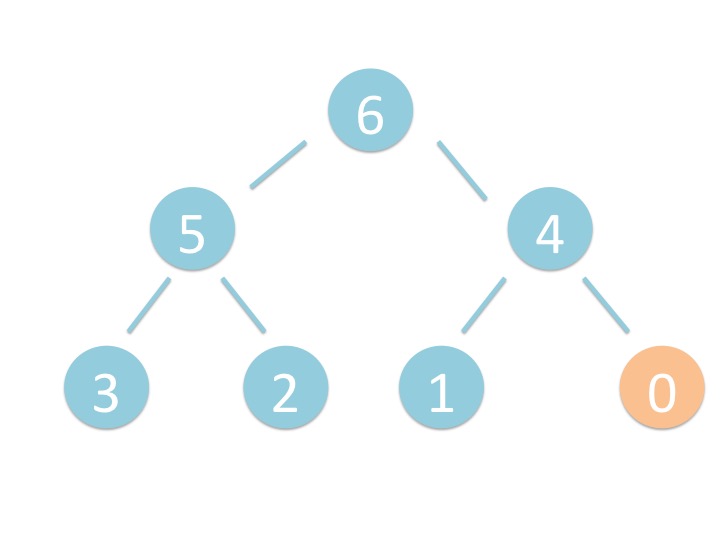
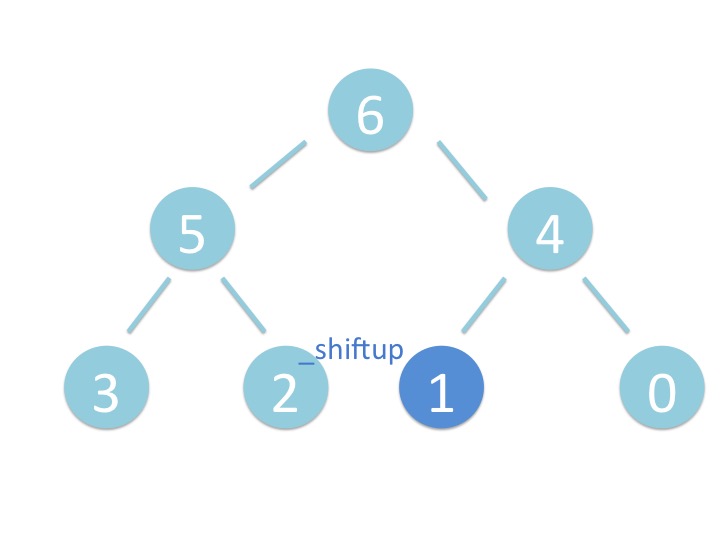
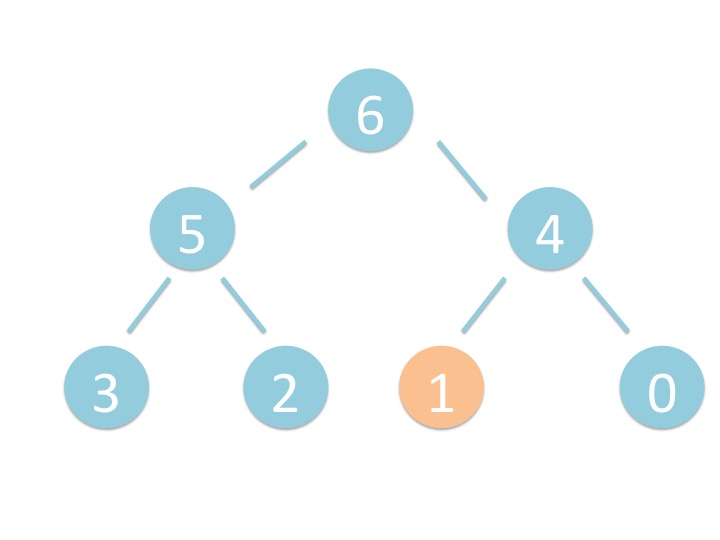
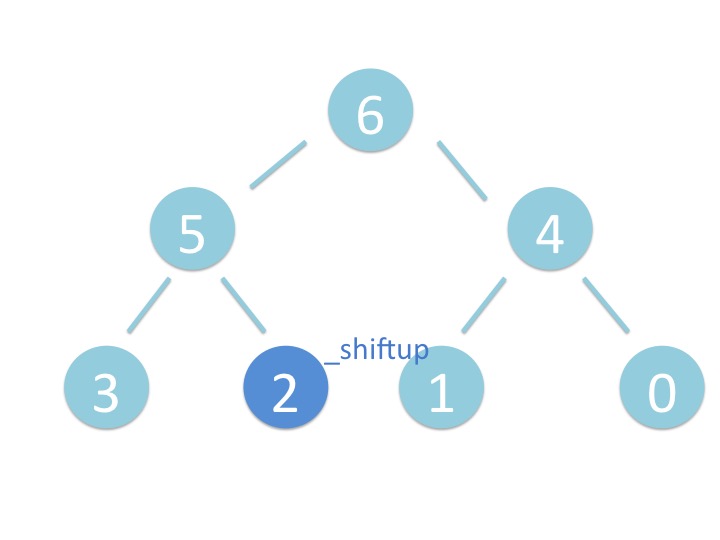
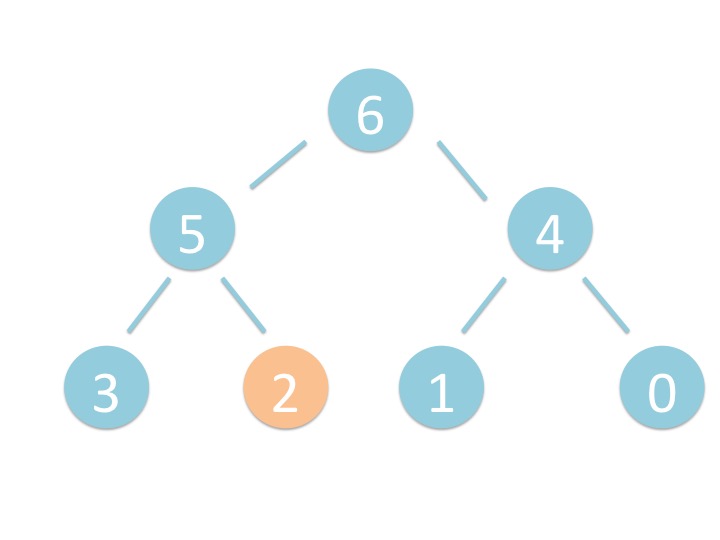
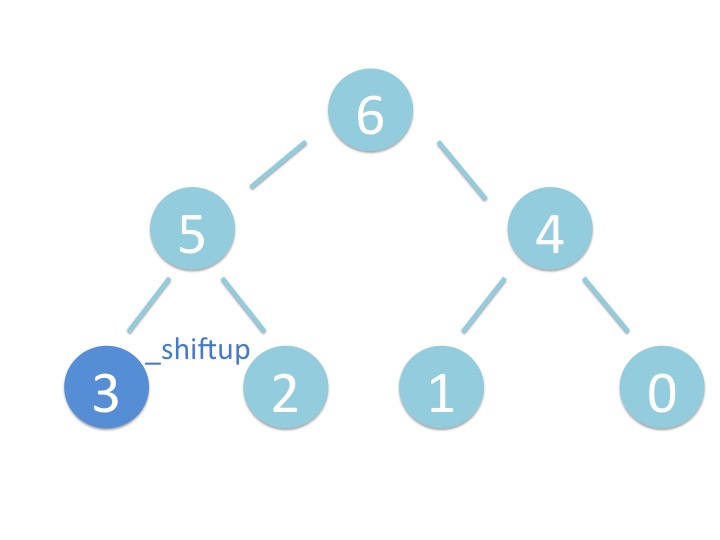
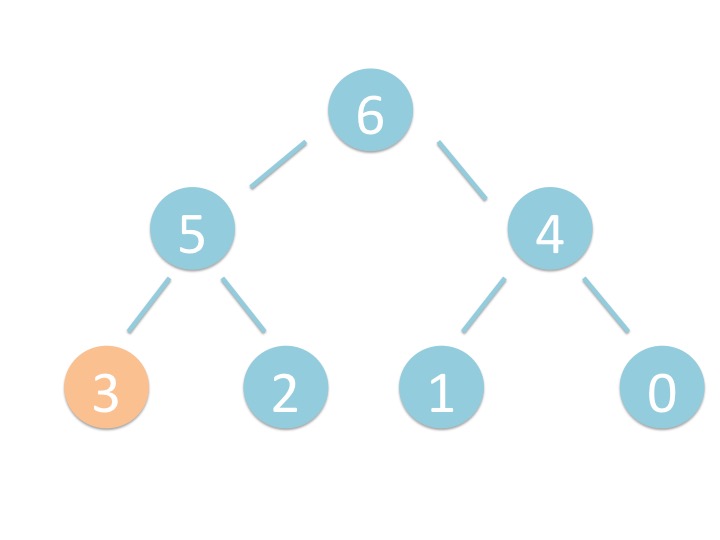
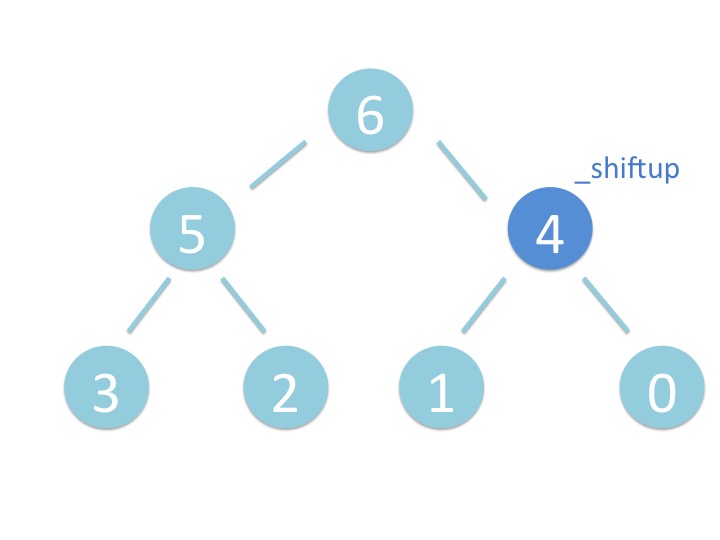
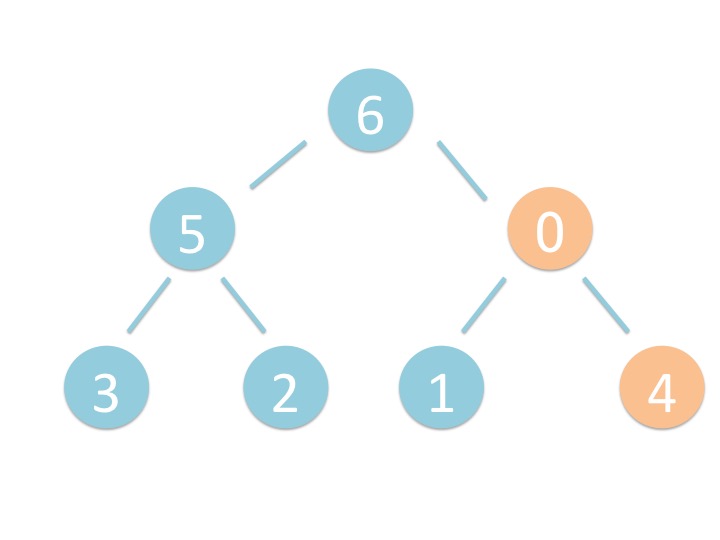
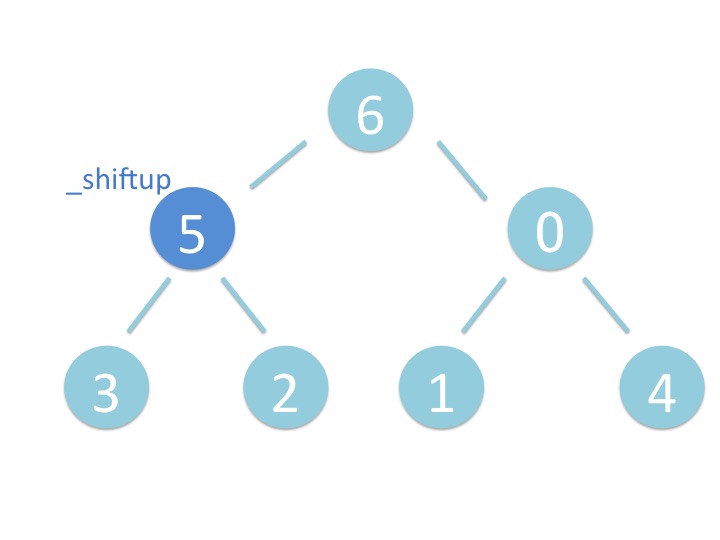
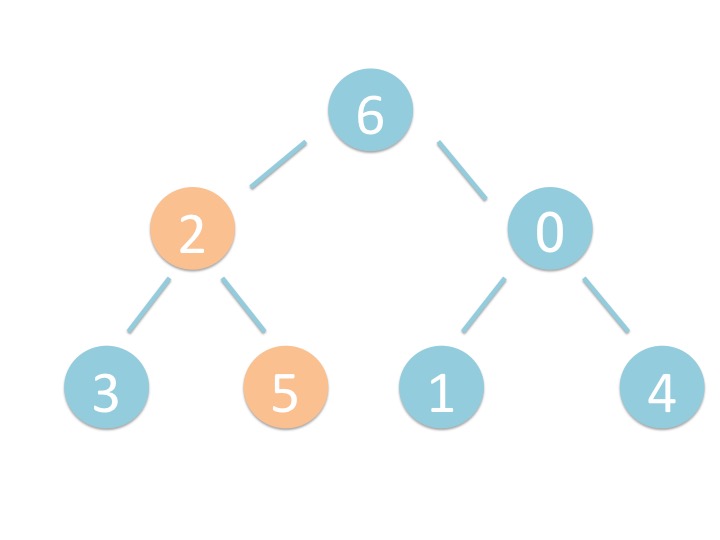
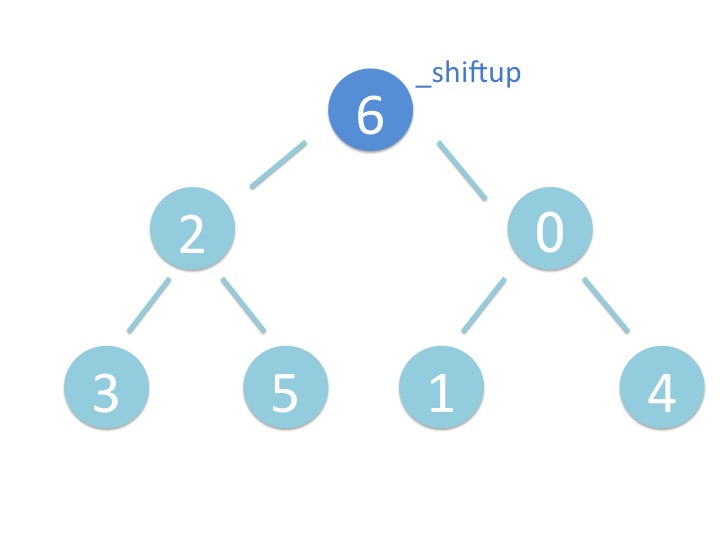
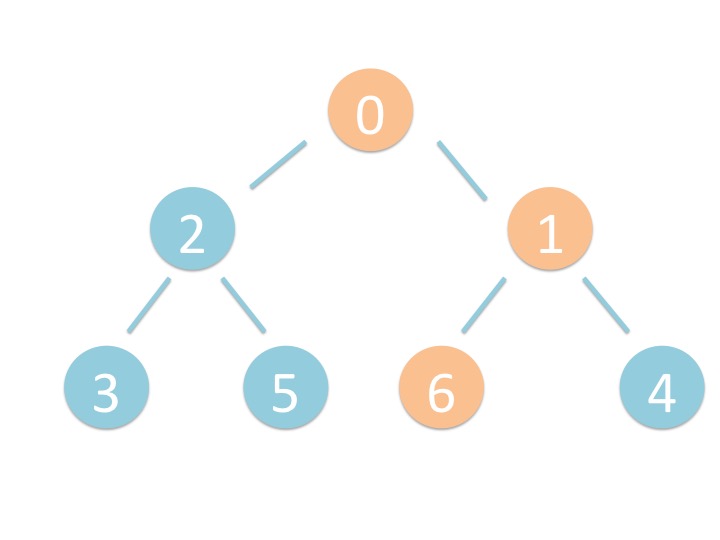
# 3.2. さわってみよう

$ git clone https://github.com/niconico25/tree
$ cd tree
$ python3  # Python の対話モードを開く

# 対話モード >>> に
# コピペで実行できます。
from tree.binary_heap.heapq import heapify

heap = [6, 5, 4, 3, 2, 1, 0]
heapify(heap)

>>> heapify(heap)



heapify: looping

_shiftup 4 -> leaf
_shiftup: before
      06      
  05      04  
03  02  01  00
_shiftup: in progress
      06      
  05      00  
03  02  01  00
_shiftup: after
      06      
  05      00  
03  02  01  04

_shiftdown 4 -> 0
_shiftdown: before
      06      
  05      00  
03  02  01  04
_shiftdown: after
      06      
  05      00  
03  02  01  04



heapify: looping

_shiftup 5 -> leaf
_shiftup: before
      06      
  05      00  
03  02  01  04
_shiftup: in progress
      06      
  02      00  
03  02  01  04
_shiftup: after
      06      
  02      00  
03  05  01  04

_shiftdown 5 -> 2
_shiftdown: before
      06      
  02      00  
03  05  01  04
_shiftdown: after
      06      
  02      00  
03  05  01  04



heapify: looping

_shiftup 6 -> leaf
_shiftup: before
      06      
  02      00  
03  05  01  04
_shiftup: in progress
      00      
  02      00  
03  05  01  04
_shiftup: in progress
      00      
  02      01  
03  05  01  04
_shiftup: after
      00      
  02      01  
03  05  06  04

_shiftdown 6 -> 0
_shiftdown: before
      00      
  02      01  
03  05  06  04
_shiftdown: after
      00      
  02      01  
03  05  06  04
>>>

# 3.3. ソースコード

コードは短いですね。range(n//2) で割っているのは、葉は不用なので枝刈りをしているためです。

def heapify(x):
    for i in reversed(range(n//2)):
        _siftup(x, i)

# 4. 問題

# 4.1. ヒープソート

heapq (opens new window) を使ってヒープソートを実装してみましょう。 heapq を使ったヒープソートのコードは、公式ドキュメントにサンプルとして書かれています。

基本的な例 - ヒープキューアルゴリズム (opens new window)

4.2. の問題は別に見る必要もないのですが、理解の確認程度にヒープソートを実装するのは悪くないかなと思ったりもします。

# 4.2. 競プロ

yukicoder でヒープを使った問題があったので、ご紹介いたします。

# 5. 終わりに

ここまで以下のような流れて二分ヒープについて見てきました。

1. ヒープとは
- ◯ 応用
- ◯ データ構造
2. サンプルコード
3. 操作の概要
4. 問題
- 4.1. ヒープソート
- 4.2. 競プロ
5. 終わりに

heapq のコード数の heappop, heappush, heapify に関わる部分は 100 行にも及ばない、ごく短いコードです。読む価値はあるかなと思ったりなかったりします。

← 木二分探索木 →