# 二分探索木で遊ぼう
# 1. 二分探索木とは
「左の子孫の値 ≤ 親の値 ≤ 右の子孫の値」という制約を持つ二分木である。 探索木のうちで最も基本的な木構造である。」だ、そうです。
# ◯ メリット
二分探索木は値の探索、データの検索を高速にします。 例えば 6 というデータを探すときに 8 -> 3 -> 6 と辿ればすぐに目的のデータが見つかります。
# ◯ デメリット
木が片方に偏ってしまう場合があります。 そのような場合は、リストと検索効率が変わらなくなってしまいます。
# ◯ 実際には...
Python の標準ライブラリには二分探索木はありません。 しかし、純粋な二分探索木であれば、 リストを用いた二分探索 で代替が効きます。 しかも、見方によっては必ず平衡を保ってくれるので、ここで実装する二分探索木よりも効果的です。
ちなみに、二分探索は標準ライブラリ bisect (opens new window) で提供されています。
じゃあなんでわざわざこんなもの書いたんだという話になりますが、 ここでは木とは何かを学習する目的で二分探索木を実装しました。
# ◯ とは言え...
とは言え完全に無駄かと言えば、二分探索木の発展系である B 木などは使われているので、 知っておいても悪くはないかなとも思います。
二分探索木を応用した B 木 B-tree などはデータベースの世界で活用されています。 二分探索木は、木というデータ構造の基礎になるものです。
この対数化を実現しているのが、実はSQLのインデックスで使われている B-tree というアルゴリズムで、 このインデックスがあるがゆえに、 テーブルの行数が10倍、1万倍、1億倍になっても性能は1億分の1ではなく8分の1ぐらいのおだやかな性能劣化で収まるのです。 こういう圧倒的なパワーこそがサイエンスと呼ぶにふさわしいものです。
MongoDBの様なNoSQLに勢いがあるのは何故ですか?SQLと比べてどんな利点や欠点がありますか? (opens new window)
# 2. サンプルコード
実装した二分探索木のコードになります。
以下は、サンプルコードです。
木は print 関数で表示できるようになっています。
試しにコードを削除して、ご自身で実装する時にも便利かなと思います。
$ git clone https://github.com/niconico25/tree
あるいは git clone コマンドでなくても直接クリックでダウンロードできたりします。
git clone あるいはダウンロードしたディレクトリを開き、対話モードを起動します。
$ cd tree
$ python3 # Python の対話モードを開く
ここから実際のサンプルコードです。
# 対話モードに
# コピペで実行できます。
# 木クラスを import
from tree.binary_search_tree import BinarySearchTree
# ノードクラスを import
# ノードの実装は 3 種類用意しました。
# これはそのうちの1種類です。
from tree.binary_search_tree.recursive import BinarySearchNode
# ノードクラスを指定して
# 木クラスをインスタンス化する。
bst = BinarySearchTree(BinarySearchNode)
#
# 1. insert
#
bst.insert(8)
bst.insert(3)
bst.insert(1)
bst.insert(6)
bst.insert(10)
bst.insert(4)
bst.insert(7)
bst.insert(14)
bst.insert(13)
print(bst)
# 08
# 03 10
# 01 06 14
# 04 07 13
#
# 2. search
#
bst.search(13).value
# 13
bst.search(11).value
# ValueError
#
# 3. list
#
bst.list()
# [1, 3, 4, 6, 7, 8, 10, 13, 14]
list(bst)
# [1, 3, 4, 6, 7, 8, 10, 13, 14]
#
# 4. delete
#
# 4.1. 削除対象の右下の子の最大値を上に持ってくる。
bst.delete_right(8)
print(bst)
# 10
# 03 14
# 01 06 13
# 04 07
# 4.2. 削除対象の左下の子の最小値を上に持ってくる。
bst.delete_left(10)
print(bst)
# 07
# 03 14
# 01 06 13
# 04
ノードの実装は3種類用意しました。 上の例では recursive.py を使用しています。
- 再帰
recursive.py - while 文
sequencial.py - while 文, 親付き
parental.py
基本的には 1 の再帰だけなんとなく知ってればいいかなと思います。 コードが一番簡単なので。 while 文の方が良い時もあるとは思うのですが、 二分探索木だけの用途であれば実際には bisect で事足りてしまうので。
# 3. 操作の概要
- 挿入 insert
- 探索 search
- 整列 list
- 削除 delete
再帰で書いたコードで解説します。 while 文で書いたものより簡単なので。
# 1. 挿入, insert
8, 3, 1, 6, 10, 4, 7, 14, 13 の順番に木に値を挿入してみましょう。 比較的これは簡単です。
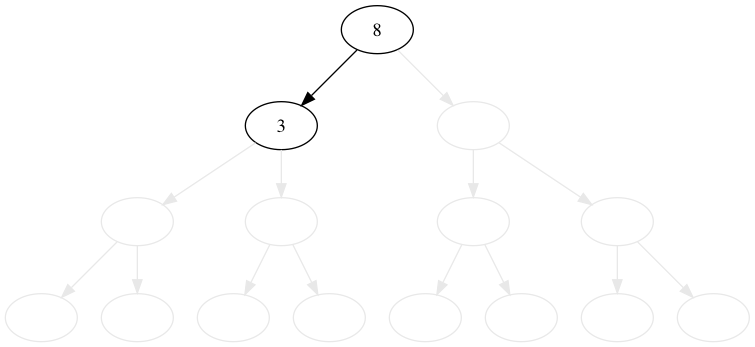
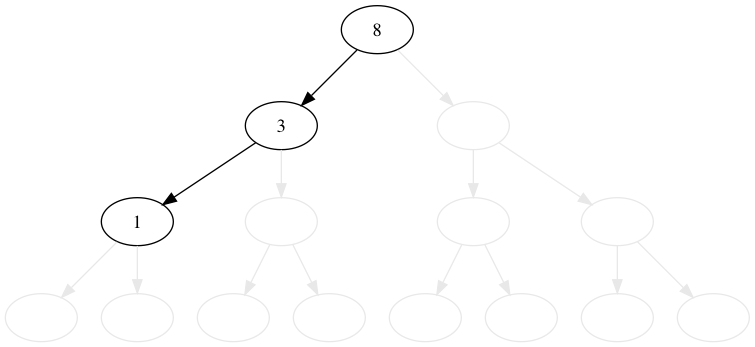
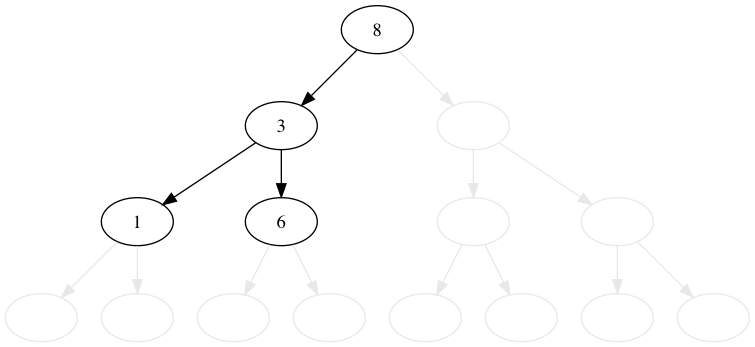
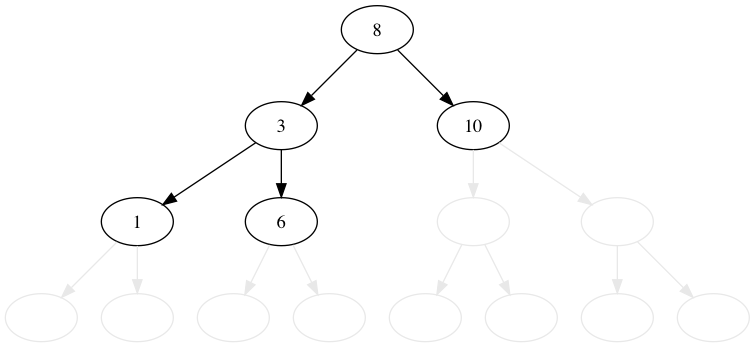
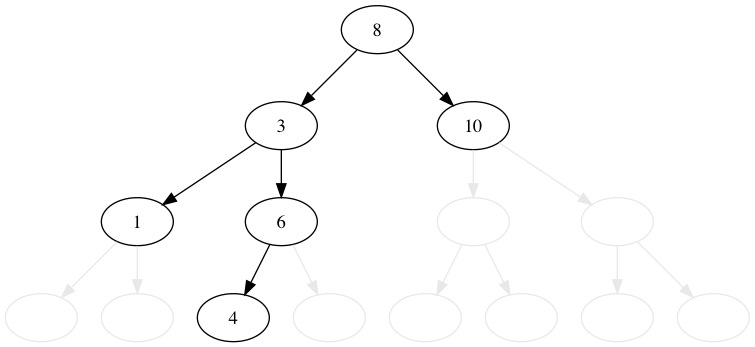
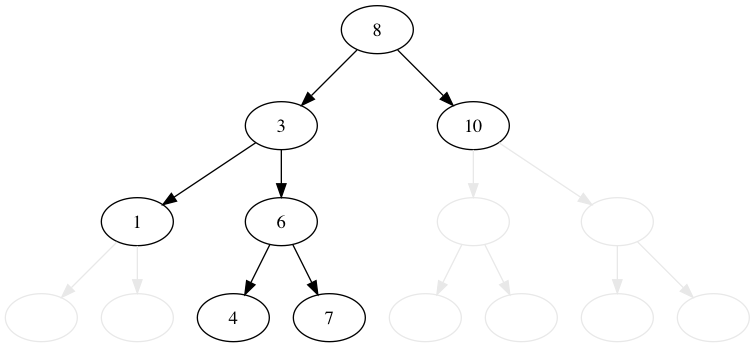
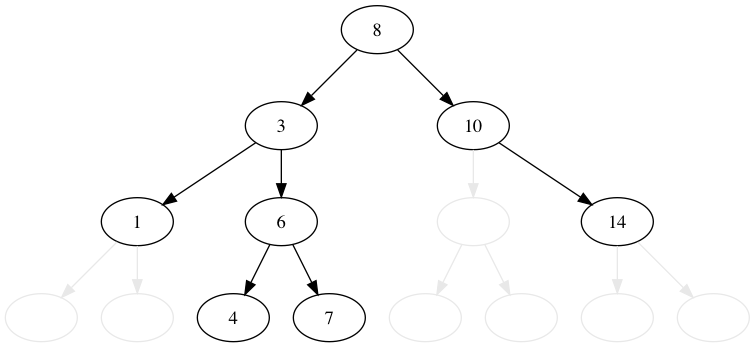
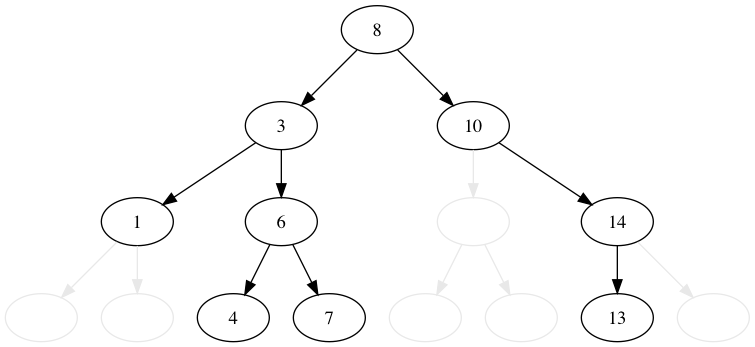
値が小さいか等しければ左へ、大きければ右に行きます。 行った先でノードがなければ、そこに新規のノードを追加します。
class BinarySearchNode:
def insert(self, value):
if value <= self.value:
if self.left:
self.left.insert(value)
else:
self.left = BinarySearchNode(value)
elif self.value < value:
if self.right:
self.right.insert(value)
else:
self.right = BinarySearchNode(value)
# 2. 探索, search
探索も挿入と同じ考え方です。
class BinarySearchNode:
def search(self, value):
if value < self.value:
if self.left:
return self.left.search(value)
else:
raise ValueError
elif value == self.value:
return self
elif self.value < value:
if self.right:
return self.right.search(value)
else:
raise ValueError
値がなかった時に raise ValueError をする方法と
return None をする方法があります。
この場合 raise ValueError がいいかなと個人的に思います。
# 3. 整列, list
二分探索木はソートされたリストを簡単に生成することができます。 2つの実装の仕方があるかなと思っています。1つ目は再帰処理。もう1つは順次処理。 すいません、作図が追いつかないので、コードで説明します。
# 3.1. 再帰処理
再帰処理で簡単にソートされたリストにすることができます。 木を潰して平らにすると自動的にソートできるイメージです。 なに言ってるんだ?って感じですが、 二分探索木を構築した時点でソートは完了しています。
>>> print(bst)
08
03 10
01 06 14
04 07 13
1 3 4 6 7 8 101314
表示した木を下にかきあつめると
ソートしたリストが出来上がります。
コードはとても簡単です。
# tree/tree/binary_search_tree/recursive.py
def BinarySearchNode:
def list(self):
# 左側の木のリスト
left = self.left.list() if self.left else []
center = [self.value]
# 右側の木のリスト
right = self.right.list() if self.right else []
return left + center + right
# ◯ コードの意味
コードの意味合いとしては、木を平らに潰すイメージです。
# 3.2. 順次処理
再帰に依らない方法は、あるのでしょうか? 1つずつ値を取り出すことはできるのでしょうか?
考え方は「次に大きな値を探す」です。次の2つの操作を繰り返します。 以下の 1, 2 の操作を繰り返せば、ソートしたリストが自動的に出来上がります。
- 右下に木があれば、右下の木の最小値を見つける。
- 右下に木がなければ、右上の親を探す。
# ◯ コードの意味
コードの意味合いとしては「深さ優先探索」でノードを辿り、 「通りがけ順 inorder」で要素を取り出しています。
再帰によらない list 関数は while 文で書きました。
知らなくても大丈夫です。
コードは複雑ですが、やっていることは上記 1, 2 の繰り返しだけです。
このコードではイテレータを使っています。
# 4. 削除, delete
ノードの削除の仕方は、2通りあります。「左の木の最大値」を削除する方法と「右の木の最小値」を削除する方法です。 二分探索木は「追加」も「探索」も「整列」も簡単なのですが「削除」になると途端に難易度が上がります...
# 4.0. 元の木
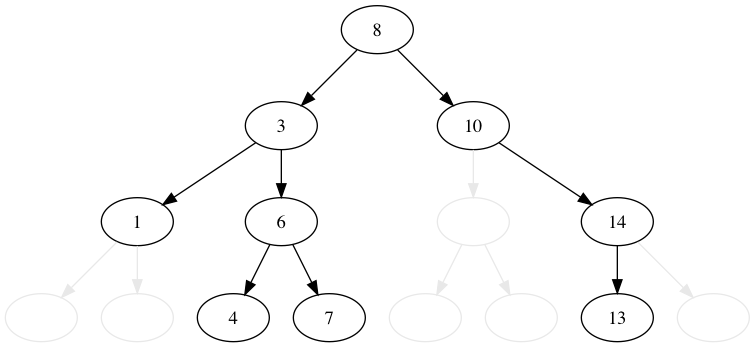
# 4.1. "8" を削除する
8 を削除するには、どうすれば良いでしょうか? 単純に削除しただけではダメで、8 がいた場所に空っぽになってしまいます。
削除対象の 8 の左の子に着目します。
例えば 6 ならどうでしょうか?6 を削除すると、 また 6 の場所が空いてしまいます。これは、なんだか面倒くさそうですね。
例えば 4 ならどうでしょうか?葉を削除するだけなので、 一見して大丈夫そうに見えますが 4 を上に持ってくると 6 が探索できなくなります。
7 は 8 がいた場所はいることができますし、 葉から抜けても木を作り直す必要はありません。
つまり「左の木の最大値」は上に持ってきても大丈夫だということです。
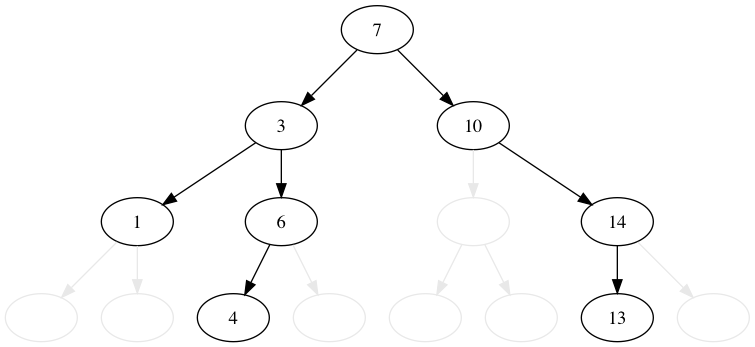
# 4.2. "7" を削除する
3 ~ 10 の間にあって葉であるノードは 4 です。 4 を持って来れば一番簡単なのですが、 ここでは「左の木の最大値」の逆「右の木の最小値」を持ってくることを考えてみましょう。 すると 10 が右の木でもっとも大きい値です。
でも安心してください。ノード 14 を上に持って来ればいいだけです。
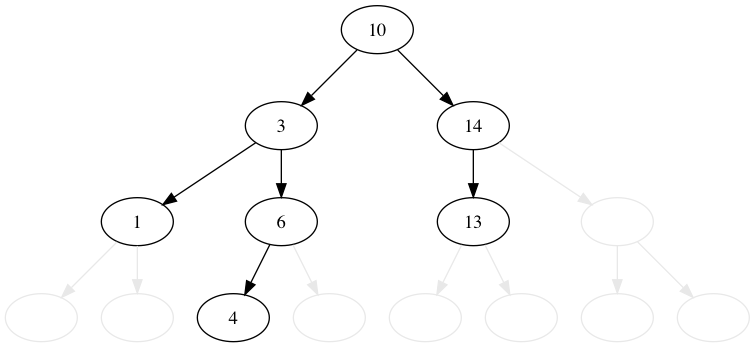
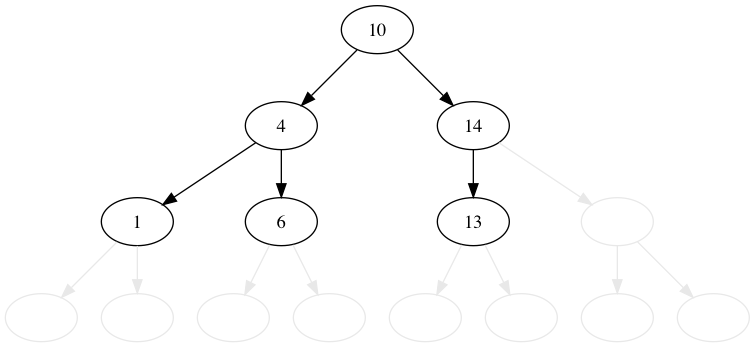
# 4.3. "3" を削除する
# 4.4. 意味
「左の子の最大値」と「右の子の最小値」とはどういう意味でしょうか? これは整列させるとわかりやすいです。 削除対象の左右どちらかの隣の値を持ってくることを意味しています。
# 対話モードに
# コピペで実行できます。
from tree.binary_search_tree import BinarySearchTree
from tree.binary_search_tree.recursive import BinarySearchNode
bst = BinarySearchTree(BinarySearchNode)
for e in 8, 3, 1, 6, 10, 4, 7, 14, 13: bst.insert(e)
print(bst)
# 08
# 03 10
# 01 06 14
# 04 07 13
list(bst)
# [1, 3, 4, 6, 7, 8, 10, 13, 14]
# 8 の左隣は 7 です。
bst.delete_left(8)
print(bst)
# 07
# 03 10
# 01 06 14
# 04 13
# 4.5. コード
class BinarySearchNode:
def delete_left(self, value):
# 1) 探索 (左の木)
if value < self.value:
if self.left:
self.left = self.left.delete_left(value)
promoted = self
else:
raise ValueError
# 2) 削除
elif value == self.value:
if self.left:
promoted = self.left._search_max()
promoted.left = self.left._delete_max()
promoted.right = self.right
else:
promoted = self.right
# 3) 探索 (右の木)
elif self.value < value:
if self.right:
self.right = self.right.delete_left(value)
promoted = self
else:
raise ValueError
return promoted
# 4. 実装の方針
よく見かける二分探索木のサンプルコードには、大きく分けて次のような違いがあります。 ここでは、何故、今回このように実装したかについて説明します。
- while 文で実装されているものと、再帰で実装されているもの。
- 親への参照 parent を持っているものと、持っていないもの。
- Node だけ実装しているものと、Tree と Node を実装しているもの。
# 1. 再帰処理か、それともwhile 文か?
再起で書いた方が簡単です。速度は while 文の方が速いです。
# 2. Node に parent を持たせるか、それとも持たせないか?
必要がなければ持たせる必要はないかなと思います。 parent を持たせるととても処理が複雑になります。
特に Python は属性を参照するだけで時間を食うので、 必要がないならば、parent という属性はない方が良いかなと思います。
速度を簡単に見ておきたいと思います。
# 1) 挿入と削除
ちゃんとしたテストではないのですが、 挿入削除を繰り返させると、 親無しの while 文 sequencial が一番速く、 ついで親ありの while 文、 最後に親無し再帰のrecursive が一番遅いです。 test_binary_search_tree.py (opens new window) にテストコードがあり、これを実行するとテストにかかった時間が表示されます。
$ python test_binary_search_tree.py
親無し再帰
### tree.binary_search_tree.recursive
..
----------------------------------------------------------------------
Ran 2 tests in 0.772s
OK
親無し while 文
### tree.binary_search_tree.sequencial
..
----------------------------------------------------------------------
Ran 2 tests in 0.496s
OK
親あり while 文
### tree.binary_search_tree.parental
..
----------------------------------------------------------------------
Ran 2 tests in 0.572s
OK
$
# 2) 整列
整列にかかる時間を計測させました。 要素をたどってソートさせるような操作は、親を持たせた方が速そうです。 説明が不十分過ぎて何やってるかさっぱりだと思うのですが、雰囲気だけ...
$ # 計測ツールをダウンロード
$ git clone https://github.com/niconico25/comparison_of_python_code
$ python3 comparison.py
# Case 5
# [randint(0, 10**5 - 1) for i in range(10**5)]
# 再帰
list_iterator : 139.0586 [msec]
# 再帰(ジェネレータ)
generator_iterator : 169.9101 [msec]
# 自作イテレータ(親なし)
original_iterator : 190.2234 [msec]
# 自作イテレータ(親あり)
original_iterator_parental : 121.0378 [msec]
# 3. Tree と Node を分けるか、それとも分けないか。
分けた方が良いと考えています。
以下、適当に読み流していただければと思います。 BinarySearchTree クラスと BinarySearchNode クラス を分けるのは実装が面倒です。 しかし、空の木を表現するときにどうしても必要になります。 これは特に削除 delete の機能を実装する場合に、必要性が顕著になります。
# 3.1. 空の木を、表現するため
空の木をどうやって、表現しますか?
もし BinarySearchTree クラスと BinarySearchNode クラスをわけなかった場合、 どうやって要素を持たない木を表現しますか? それには2つのやり方があると思います。
# 1) 代替案 None
1つ目は None を値を持たない木であるとすることです。 しかしそうすると、1度、木が空に None になってしまうと、もう木という型ではなくなってしまいます。 結果的に insert, list と言った処理が実行できなくなります。
from tree.binary_search_tree.recursive import BinarySearchNode
# ノードを木に見立てて生成する。
bst = BinarySearchNode(8)
bst.insert(3)
bst.insert(1)
bst.insert(6)
bst.insert(10)
bst.insert(4)
bst.insert(7)
bst.insert(14)
bst.insert(13)
# 木を空にする。
# 欠点 1
# 削除すると根が変わるので
# 削除のたびに代入しないといけない。
bst = bst.delete_left(8)
bst = bst.delete_left(3)
bst = bst.delete_left(1)
bst = bst.delete_left(6)
bst = bst.delete_left(10)
bst = bst.delete_left(4)
bst = bst.delete_left(7)
bst = bst.delete_left(14)
bst = bst.delete_left(13)
# 欠点 2
# 木を空にすると None になる
# もう insert はできない...
# AttributeError
assert bst is None
bst.insert(3)
# 2) 代替案 BinarySearchNode(None)
2つ目は None を値に持つ BinarySearchNode を空の木と見立てることです。 これなら空になっても insert などの処理は実行できそうです。
class BinarySearchNode:
# insert メソッドが少しだけ、複雑になるだけで済む。
def insert(self, value):
if self.value is None:
self.value = value
elif value < self.value:
if self.left:
self.left = BinarySearchNode(None)
self.left.insert(value)
else:
if self.right:
self.left = BinarySearchNode(None)
self.right.insert(value)
なんだか上手くいきそうですね。次のことを考えてみましょう。
# 3.2. ルートを削除したときの対応のため。
2つ以上の変数または属性から、木が参照されているシーンについて考えると、もう逃げられなくなります。 削除の操作をした時に、根を変数、属性に代入できれば良いのですが。
from tree.binary_search_tree import BinarySearchNode
# BinsarySearchNode を木に見立てる...
bst = BinarySearchNode(8)
bst.insert(3)
bst.insert(1)
bst.insert(6)
bst.insert(10)
bst.insert(4)
bst.insert(7)
bst.insert(14)
bst.insert(13)
# あるオブジェクトに bst を登録する。
dct1 = {'tree': bst}
dct2 = {'tree': bst}
print(dct1['tree'])
# 08
# 03 10
# 01 06 14
# 04 07 13
# 8 を削除すると...
bst.delete_left(8)
# 8 しか表示されない...
print(dct1['tree'])
# 08
print(dct2['tree'])
# 08
# これは面倒すぎる...
# dct1['tree'] = dct2['tree'] = bst.delete_left(8)
# 3.3. まとめ
空の木を表現するには Node と Tree を分けた方が良さそうです。
# 5. 代替案
実はソートについてはクイックソートで、 探索については二分探索で、それぞれ二分探索木と似たようなことができます。
ソートについては Python には list.sort メソッドと sorted 関数があるので、
わざわざクイックソートを自分で実装しようと思うことはないかなと思います。
しかし、探索については二分探索木を実装しようと思ってしまうかもしれません。
標準ライブラリに bisect があるので、これを使えばいいかなと思います。
# 1. 二分探索 bisect
二分探索木には、どのような利点があるのでしょうか?
二分探索木は、二分木に対して、 あるルールを適用することによって、 データの探索効率を向上させたデータ構造です。
二分探索木 - Programming Place Plus アルゴリズムとデータ構造編 (opens new window)
実は、わざわざ二分探索木を実装しなくても、 ソートされたリストを用いて同じことができます。この方法を二分探索と言います。
実は Python では二分探索を行う bisect と言う組み込みモジュールを提供してくれています。
random_list = [8, 3, 1, 6, 10, 4, 7, 14, 13]
sorted_list = sorted(random_list)
print(sorted_list)
# [1, 3, 4, 6, 7, 8, 10, 13, 14]
"""
1. bisect
ソートされた順番を崩すことなく
要素を挿入できる。
"""
import bisect
bisect.insort_left(sorted_list, 11)
print(sorted_list)
# [1, 3, 4, 6, 7, 8, 10, 11, 13, 14]
"""
2. 二分探索木
ソートされた順番を崩すことなく
要素を挿入できる、と考えることもできる。
"""
binary_search_tree = BinarySearchTree()
binary_search_tree.insert_iterable(random_list)
binary_search_tree.insert(11)
print(list(binary_search_tree))
# [1, 3, 4, 6, 7, 8, 10, 11, 13, 14]
二分探索木と二分探索は異なるものです。 二分探索木はデータ構造です、 二分探索はソートされたリストを活用したアルゴリズムです。
二分探索木では平衡状態を保つためには、木の回転の操作などが必要になります。 ソートされたリストは平衡状態を保った二分探索木であると考えることもできます。 リストを用いた二分探索 bisect を用いれば、平衡状態を保つために木の回転をする必要がありません。
また、bisect モジュールを用いればソートされたリストを高速に検索することもできます。
# 2. クイックソート
二分探索木を使ったソートは、基本的にはクイックソートと同じことをしています。
クイックソートは、基準になる値を1つ決め、それより大きい値のグループと小さい値のグループに分けます。そしてこの作業を繰り返し、ソートされたリストを得ます。それは、ちょうど二分探索木が、挿入された要素を左側の子と右側の子に振り分ける動作と、とてもよく似ています。
実際、クイックソートのコードは、二分探索木からリストを生成するコードとそっくりです。
def quick_sort(lst):
if not lst:
return []
# 1.
smaller_sorted_list = quick_sort([e for e in lst[1:] if e <= lst[0]])
center = lst[0]
bigger_sorted_list = quick_sort([e for e in lst[1:] if e > lst[0]])
# 2.
sorted_list = smaller_sorted_list + [center] + bigger_sorted_list
# 3.
return sorted_list
lst = [8, 3, 1, 6, 10, 4, 7, 14, 13]
print(quick_sort(lst))
クイックソートは名前の通り、基本的には高速にソートを行えます。 しかし、データに偏りがあったりすると、高速にソートできません。 このような性質は、これは二分探索木と同じですね。
ちなみに Python のソートアルゴリズムには TimSort が実装されているそうです。 いろんなソートアルゴリズムを掛け合わせているようです。
# 6. 参考
削除の実装に当たって、次のサイトを参考にしました。 削除した木のルートを返すと色々と上手くいくことを学びました。
